GAMES101现代计算机图形学入门

Lecture 01 Overview of Computer Graphics

What is Computer Graphics?

图形学在动画，电影，游戏，设计，可视化，VR，数字插画，模拟，GUI，字体等领域均有应用

最难做的往往是日常生活中最常见的东西

Why Study Cmputer Graphics?

• Fundamental Intellectual Challenges
• Technical Challengs
• Forget about the previous reasons
  **Computer Graphics is AWESOME! **

Course Topics

Rasterization(光栅化)

光栅化：把三维空间的几何形体显示在屏幕上

Curves and Meshes

Ray Tracing（光线追踪）

慢，但能达到好的效果

Animation/Simulation

games101 is NOT about

• Using OpenGL/DirectX/Vulkan
• The syntax of Shaders
• We Learn Graphics, not Graphics APIs!
• After this course you’ll be able to learn these by yourself
• 3D modeling and GameEngine
• Computer Vision/Deep Learning

Course Logistics

General Information

//关于课程网站，教学资料什么的
推荐书籍：Fundamentals of Computer Graphics（虎书）

Use An IDE！

Lecture 02 Review of Linear Algebra

Graphics’ Dependencies

• Basic mathematics
• Basic physics
• Misc:Signal processing/Numerical analysis
• A bit of Aesthetics

//讲了一些简单的线性代数，我酌情跳过了一些

点乘可以计算两个向量的夹角，接近程度
如果有a·b，则b-bcos（a，b）与bcos（a，b）垂直

本课的叉乘用的是右手系

叉乘可以判定左右，内外

Lecture 03 Transformation

2D transformations

Sclale

对角阵可以作为缩放变换矩阵

reflection matrix

eg.
horizontal reflection: x‘ = -x，y’ = y

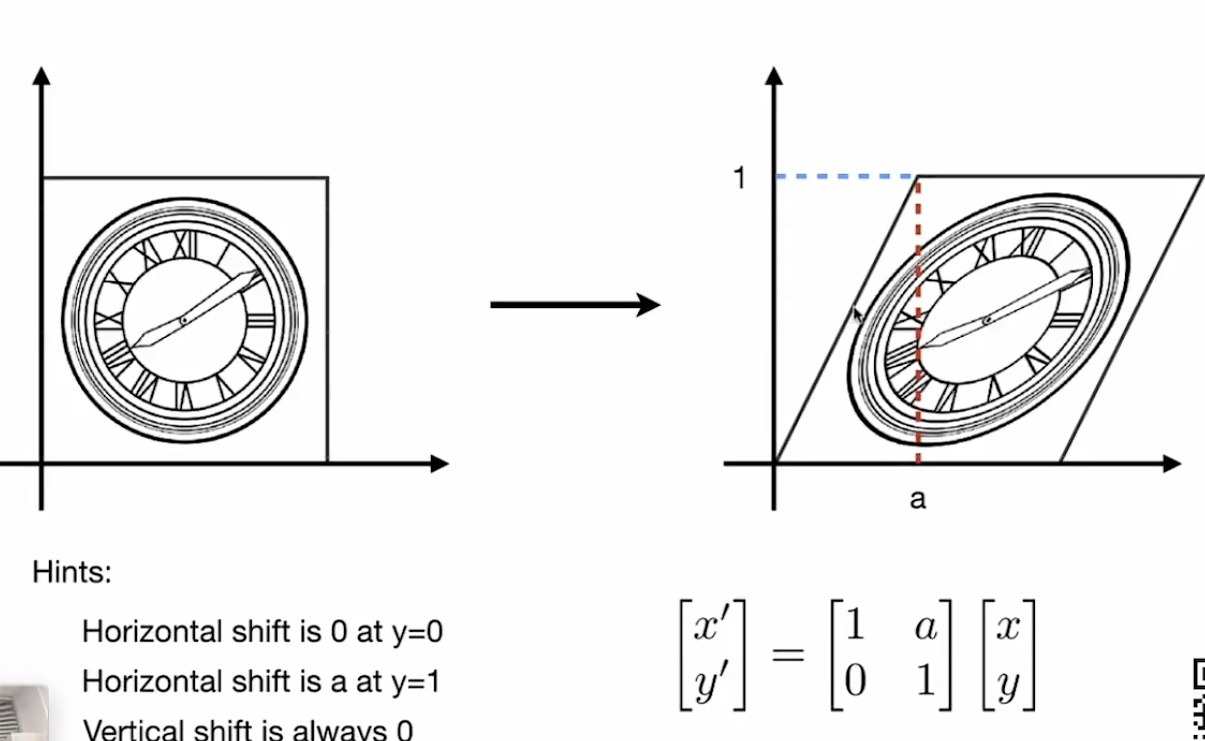
Shear matrix

运用特定种类的矩阵发生的变换

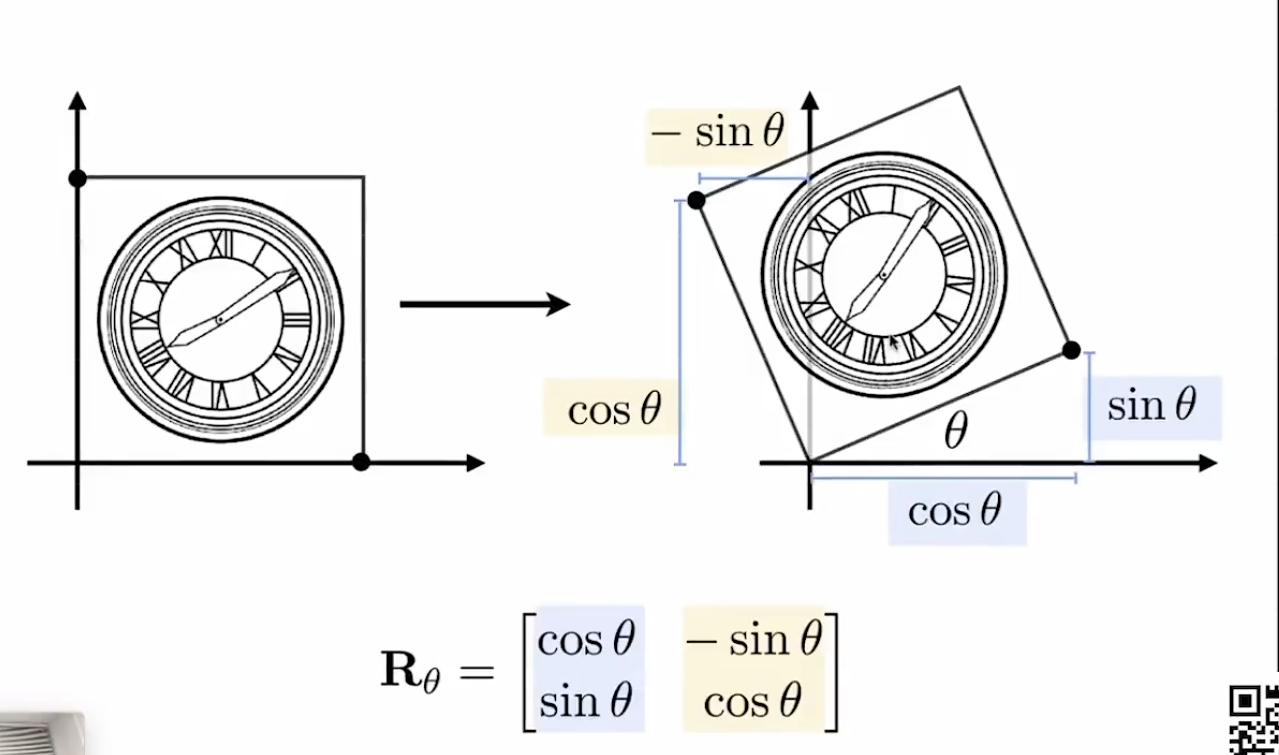
Rotate

Homogeneous coorinates

关于平移变换：
当我们想到平移变换的表示，直观的想法是（x，y）+（a，b），但这种表示法不能用矩阵乘向量的形式表示,所以我们要引入齐次坐标

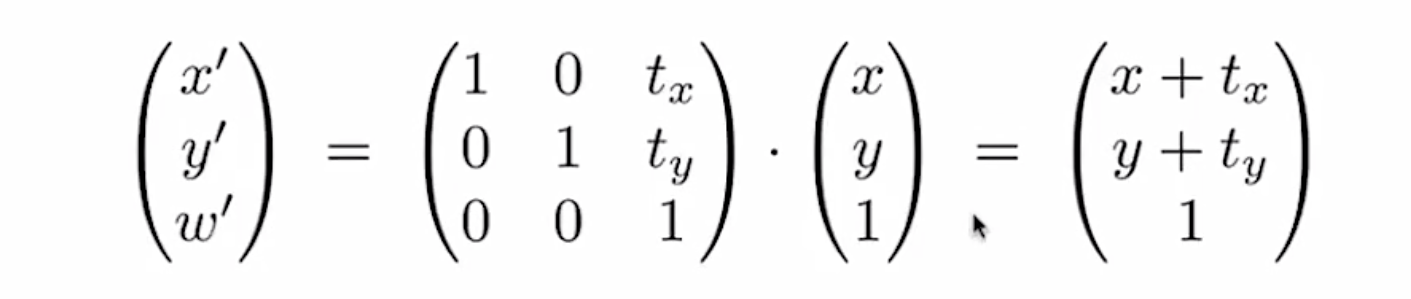
Affine Transformations

• 仿射变换:线性变换和平移变换的叠加

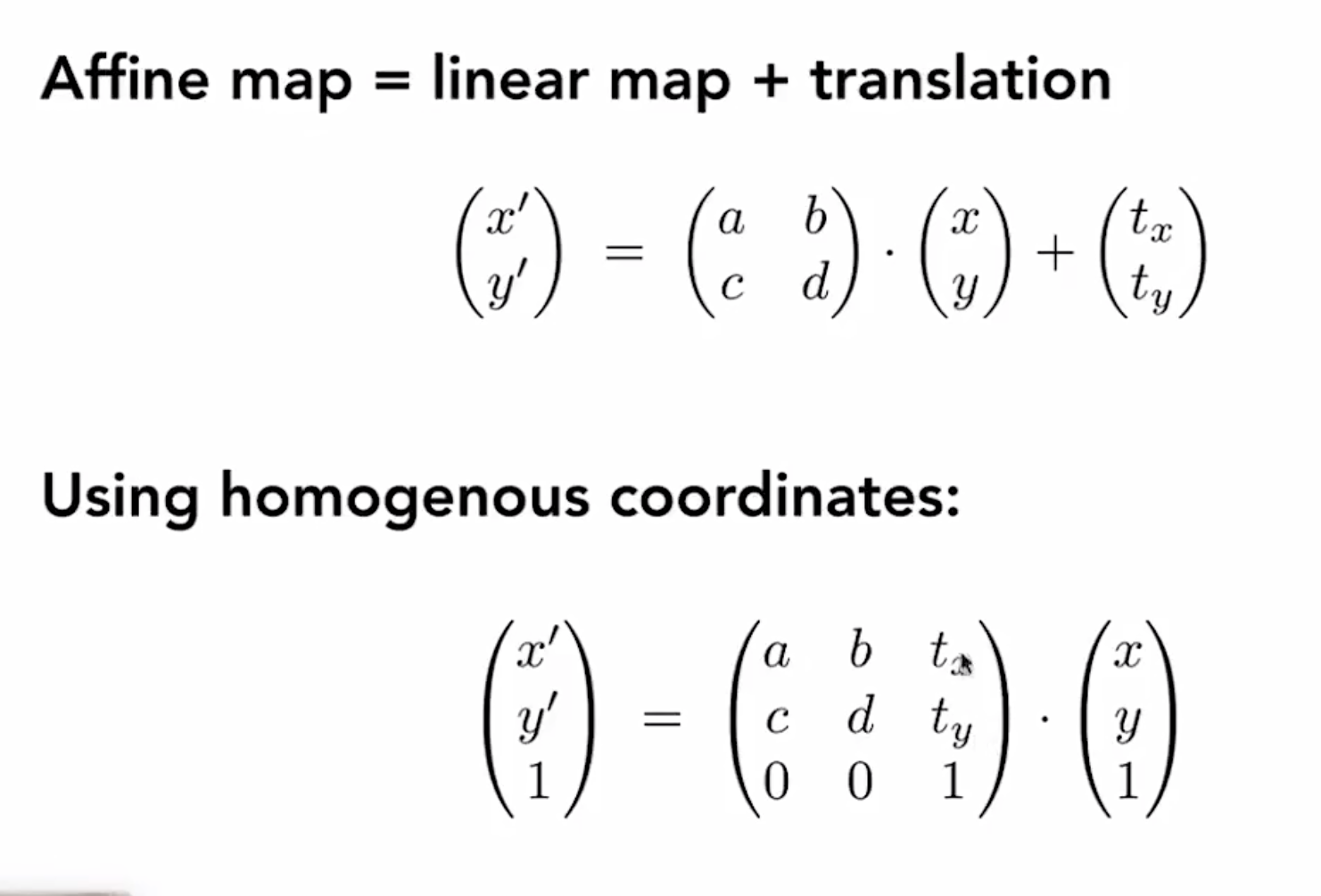
顺序:先线性变换再平移

Inverse Transform

Composite Transform

变换的顺序非常重要,矩阵乘法没有交换律

变换应用的顺序是从右到左

Decomposing Complex Transforms

如果有一个正方形,取其一点a(x,y),绕其旋转,我们可以现将正方形移动-a,也就是将a点移动到原点,进行旋转,然后再移动a,就得到了结果

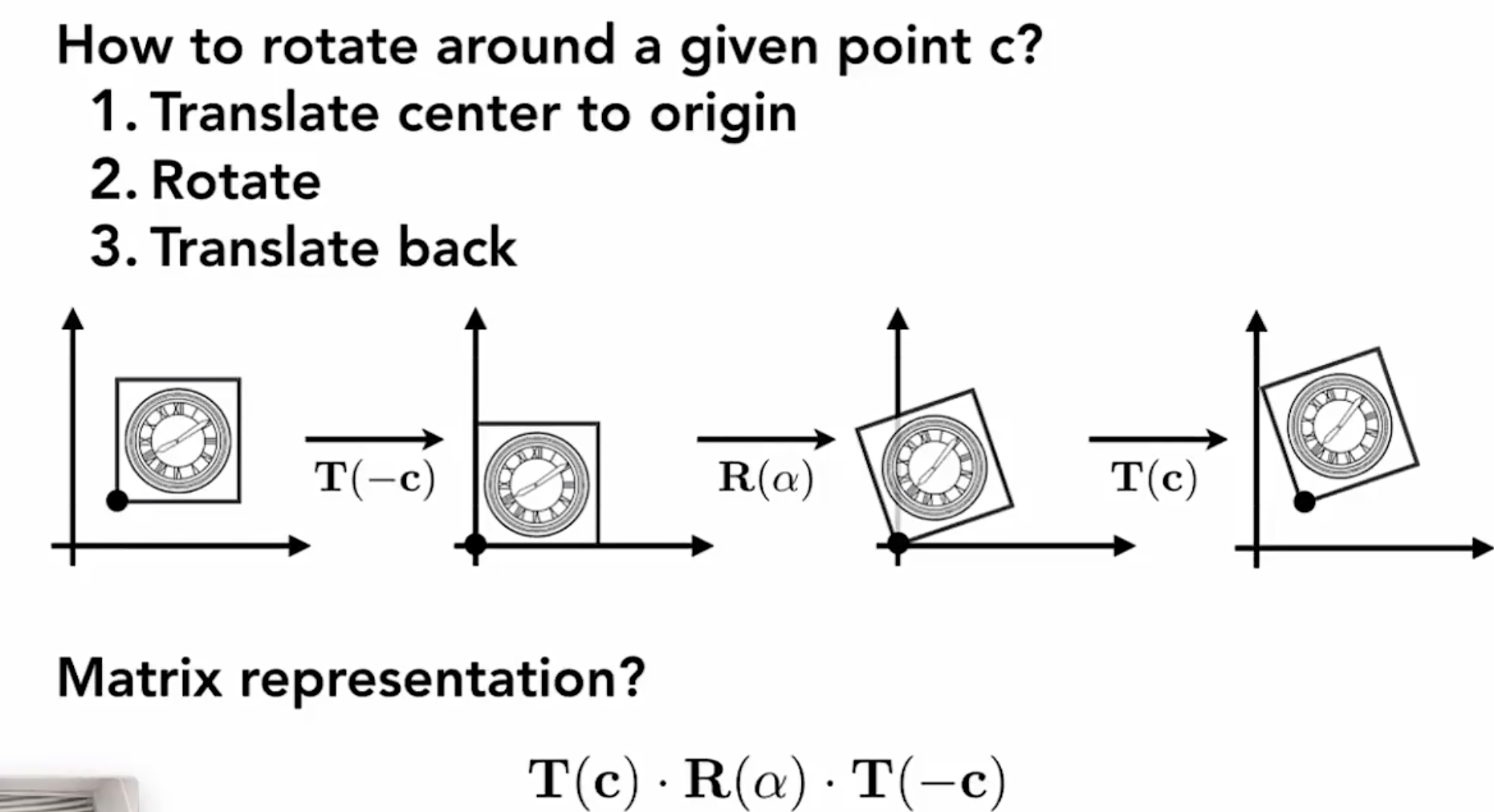
3D Transformatios

//大概意思是和2D类似

Lecture 04 Transformation Cont

对上节课的补充:旋转矩阵的逆等于旋转矩阵的转置,都表示旋转负角度

数学上一个矩阵的逆等于它的转置,那么我们称它为正交矩阵

3D Transformatios

三维的旋转

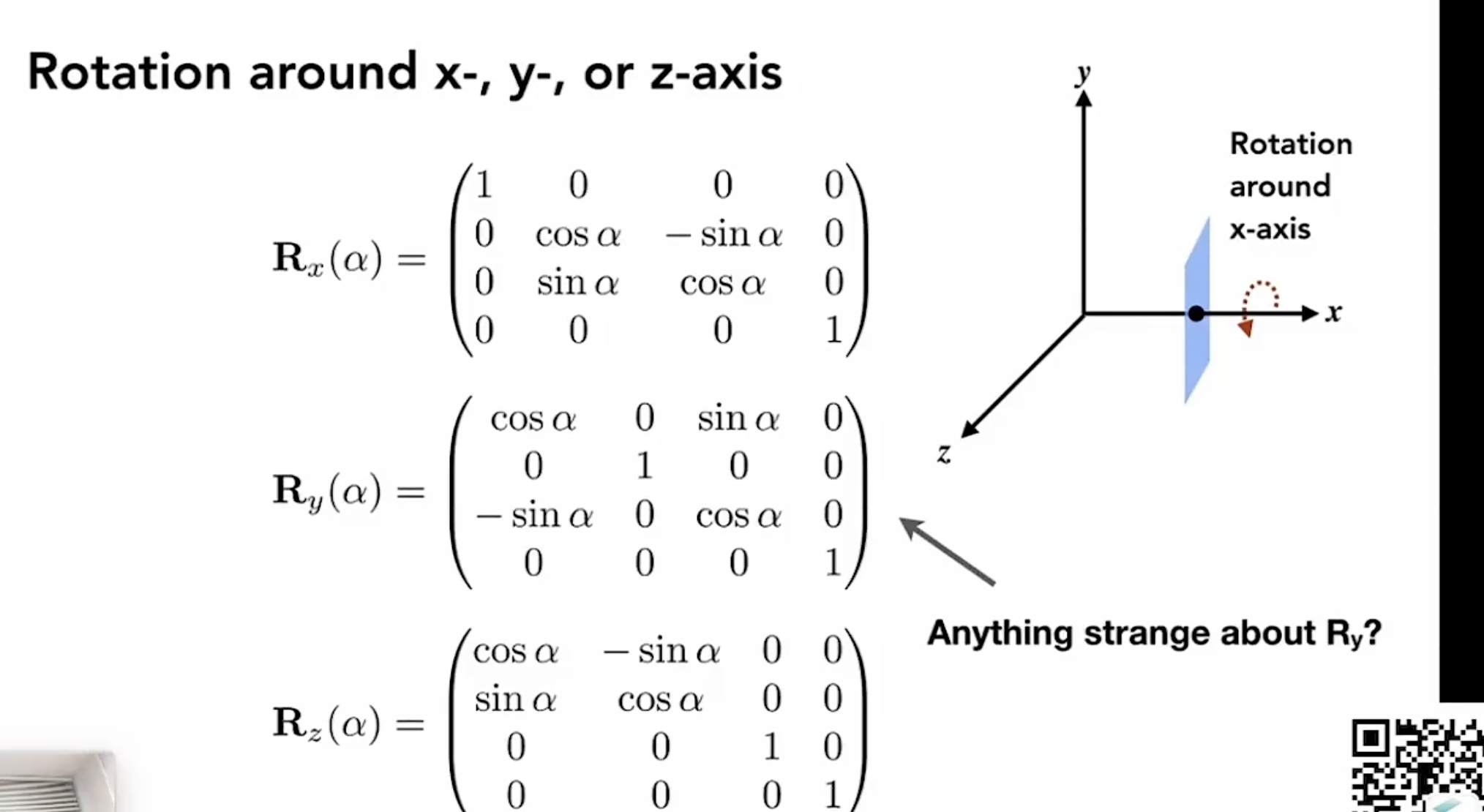
欧拉角

绕任意轴的旋转可以转换成绕xyz轴的复合旋转

Rodrigues’Rotation Formula

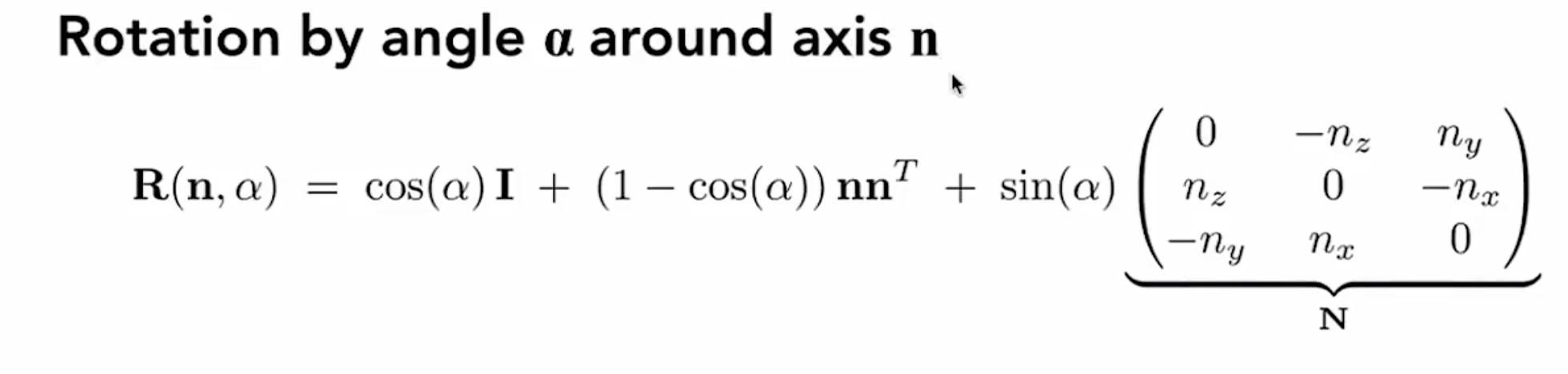
Viewing transformation

View/Camera trnasformation

我们希望把三维的图形转化为二维的视图

• What is view transformation?

  MVP变换 找到模型,改变相机的位置,方向,将三维的图形投影到摄像机

• Defne the camera first

  Position e

  Look-at/gaze direction g

  Up direction t

• Key observation

  如果相机和所有的东西共同运动,那么视图是保持不变的

  那么我们就可以认为,相机永远在原点,而所有的视图的变化都是物体的变换造成的

  把相机放到标准位置有好处,但也会造成一定的问题

• Transform the camera by Mview

  So it’s located at the origin ,up at Y, look at-Z

• Mview in math?

  Translates e to origin

  Rotates g to -Z

  Rotates t to Y

  Rotates (g 叉乘 t ) To X

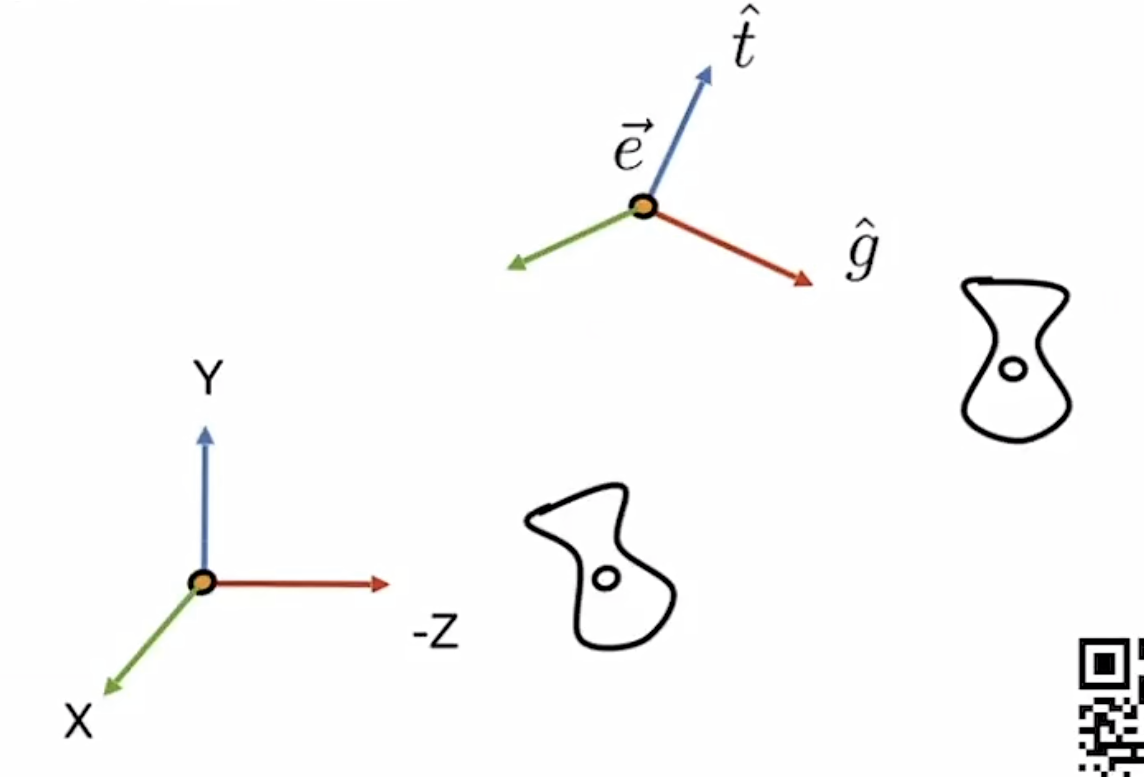
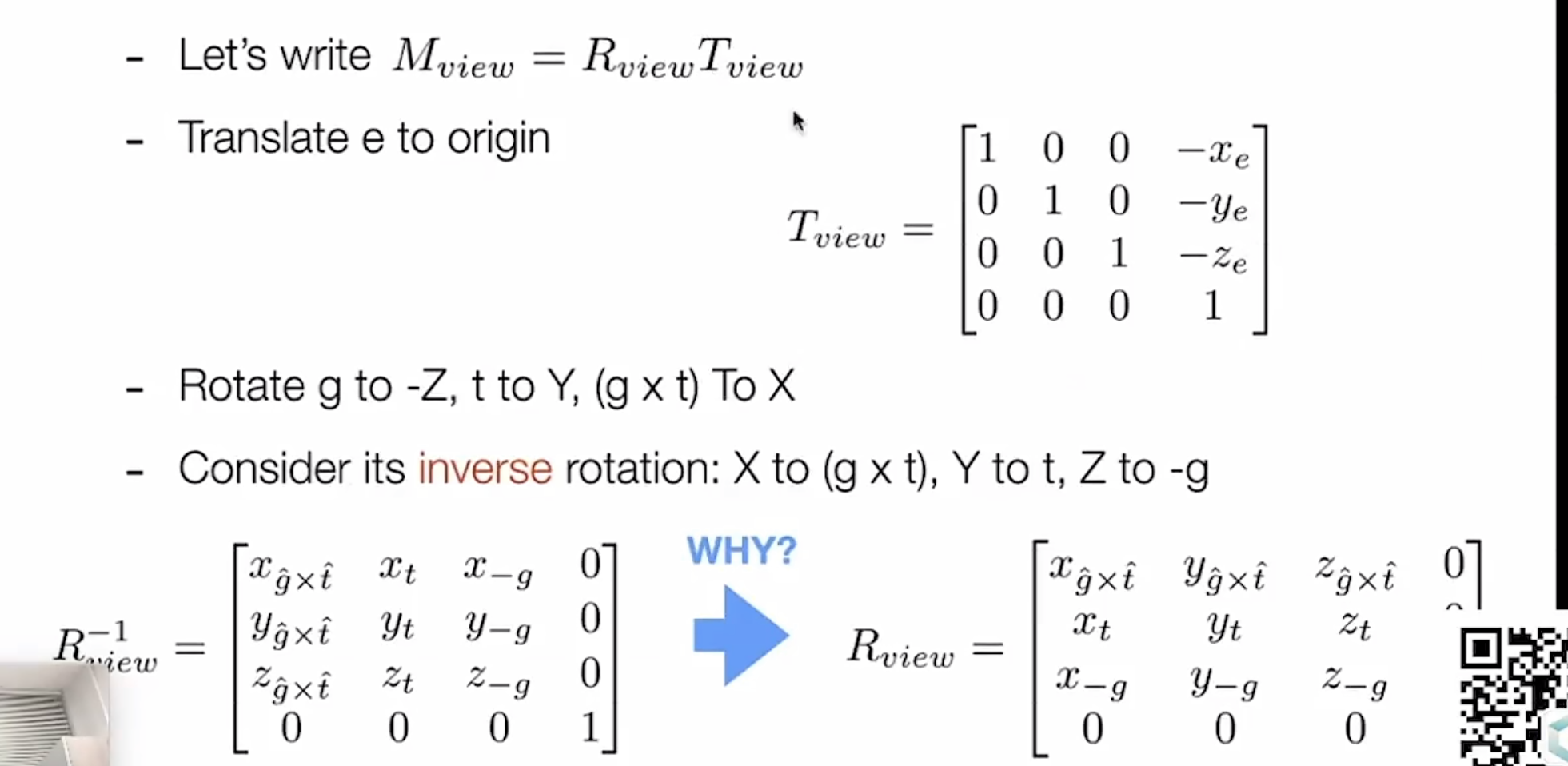
所以我们要对Rview矩阵求逆,还记得吗,旋转矩阵的逆就是它的转置

Projuction transformation

Orthographic projection

• A simple way of understanding

  camera located at origin ,looking at -Z, up at Y

  Drop Z coordinate

  Translate and scale the resulting rectangle to [-1,1]^2(一个原定俗成的做法,简便之后的计算)

• In general

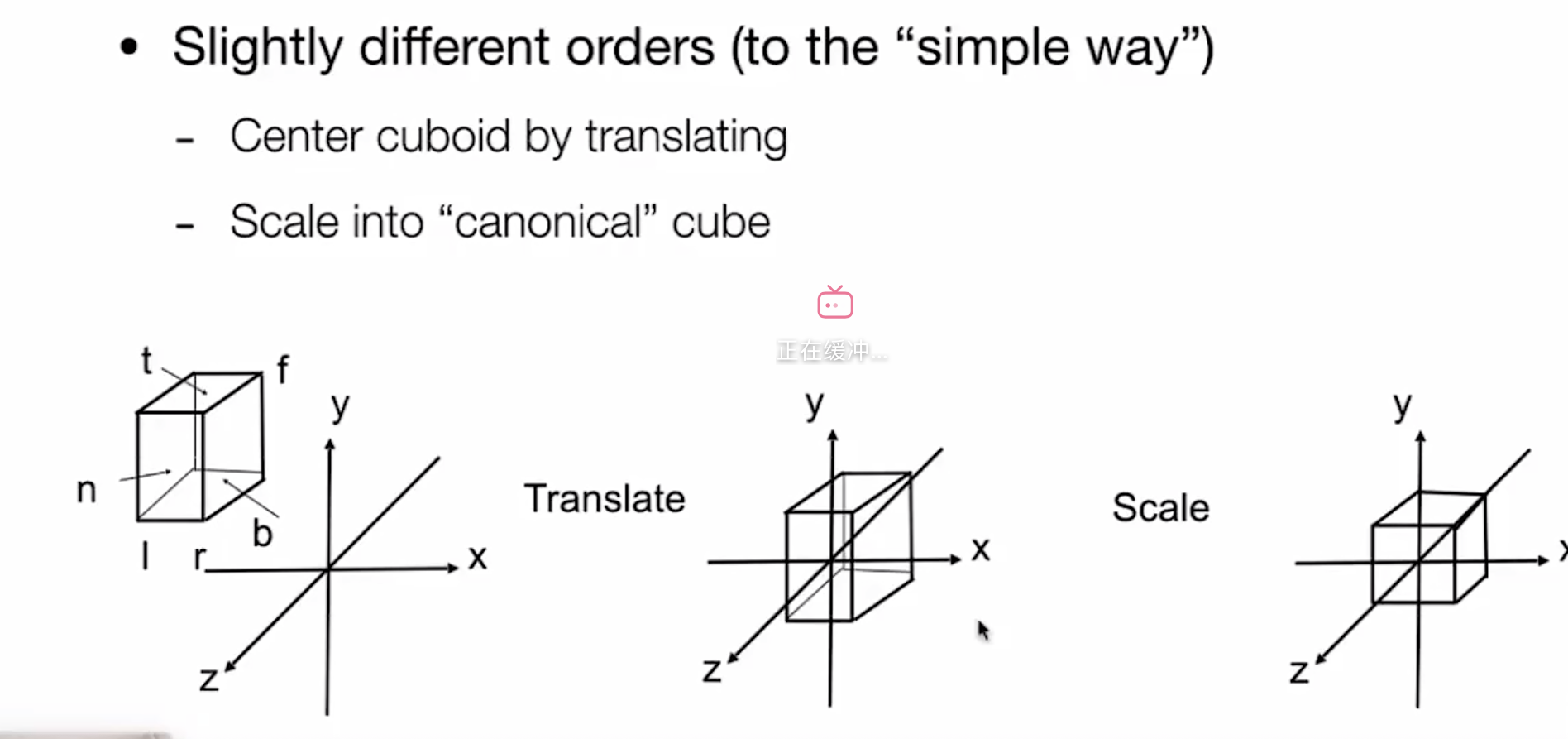
再次确认,本课我们坚持右手系

Perspective Projection

近大远小

首先回忆一些知识

如果k是任意的,那么k就可以是z

表示正交投影,可以将远处的4点”挤”成和近处4点一样大的形状,再进行一次正交投影

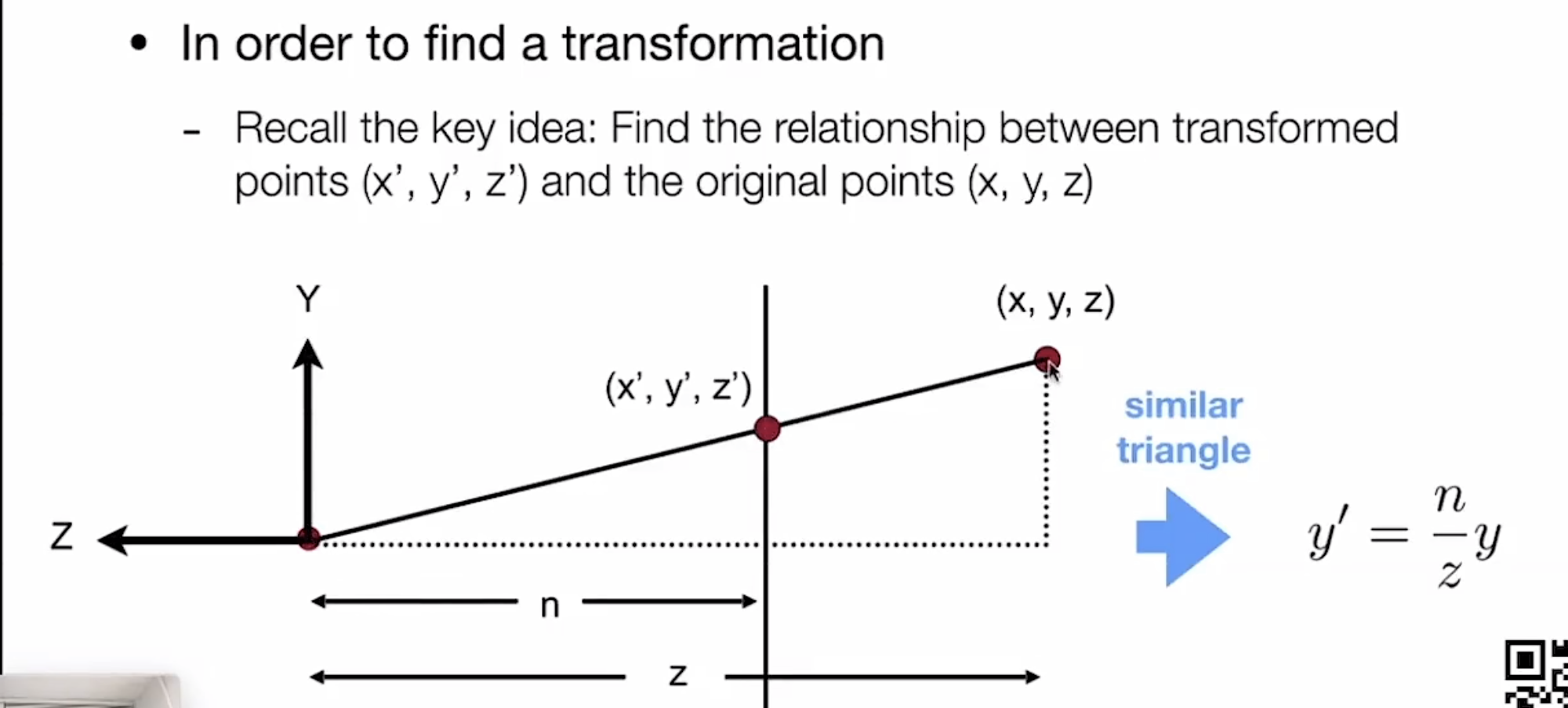
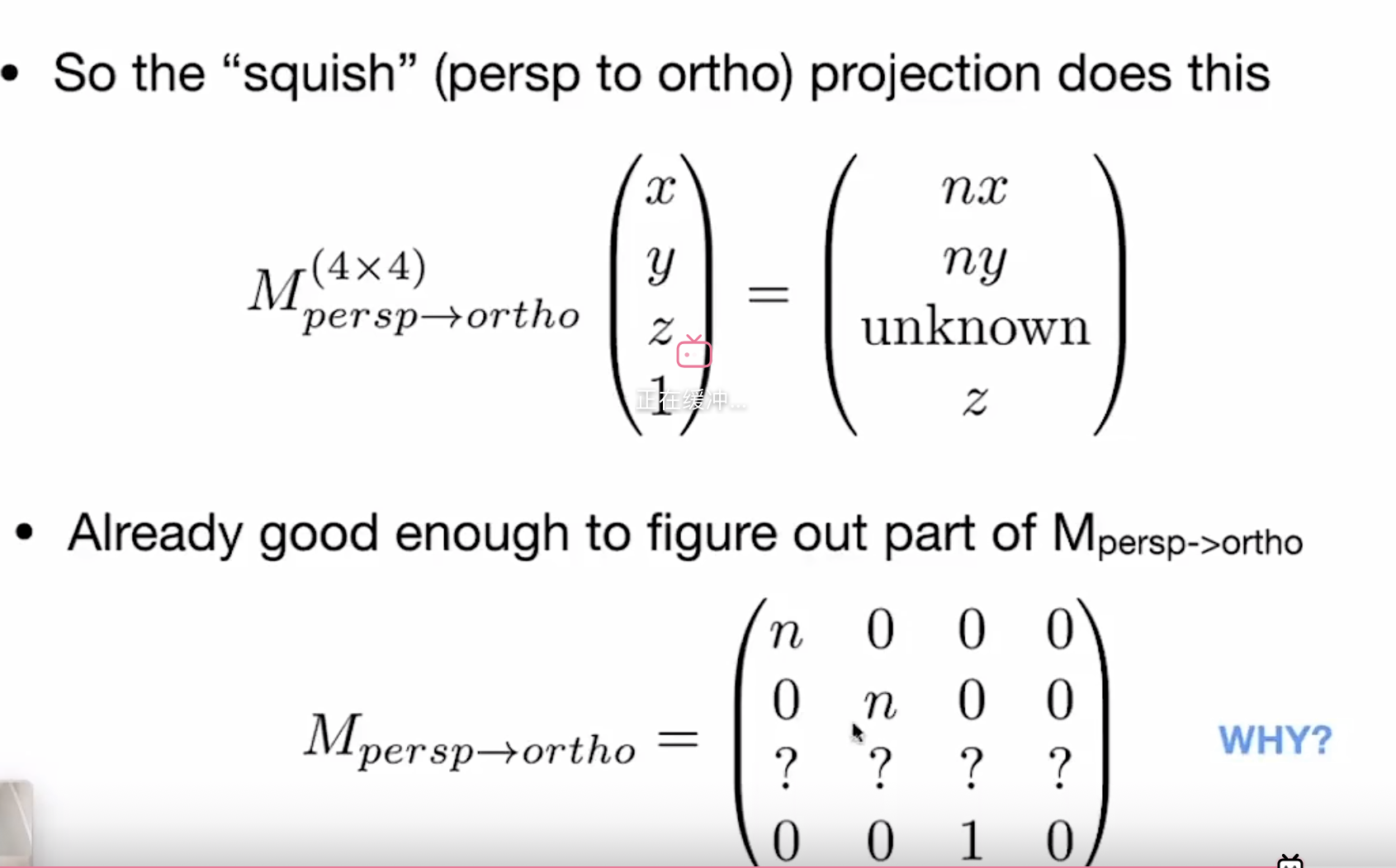
此时我们需要明确:进出的点不会变化,远处的点的z也不会变化

用f表示远处点z的值

Lecture 05 Rasterization 1(Triangles)

如果我们想定义一个视锥,可以只定义一个可视角度和一个宽高比

• What after MVP?

Canonical Cube to Screen

• What is a screen?

  an array of pixels

  Size of the array: resolution

  Atypical kind of raster display

• Rasterize(光栅化) == drawing onto the screen

• Defining the screen space

  认为屏幕的左下角是原点,屏幕中所有的像素用(x,y)表示

  Pixel’s indices are from (0,0)to (width-1,height-1)

  Pixel(x,y) is centered at (x+0.5,y+0.5)

  the screen covres range (0,0)to (width,height)

  我们先简单的认为像素是内部颜色均匀的小方块

Triangles-Fundamental Shape Primitives

• Why triangles?

  Most basic polygon

  Break up other polygons

  Guaranteed to be planar

  Well-defined interior

  Well-defined method for interpolating values at vertices over triangle

Sampling a Funation

简单的光栅化做法:采样-给你一个函数,你给它不同的x,求不同的值

在光栅化的过程中,我们对像素中心进行采样,判断一个像素是否在三角形内,这里应用叉乘

We sample time(1D),area(2D),direction(2D),volume(3D)

Lecture 06 Rasterization2(Antialiasing and Z-Buffering)

在采样后,如果屏幕的像素不高,那么我们会得到一个”走样”的图形,如何抵消锯齿感的技术就是抗锯齿(反走样)

• 一种简单的反走样方法

  对原来的图形做模糊(滤波),然后再对它进行采样

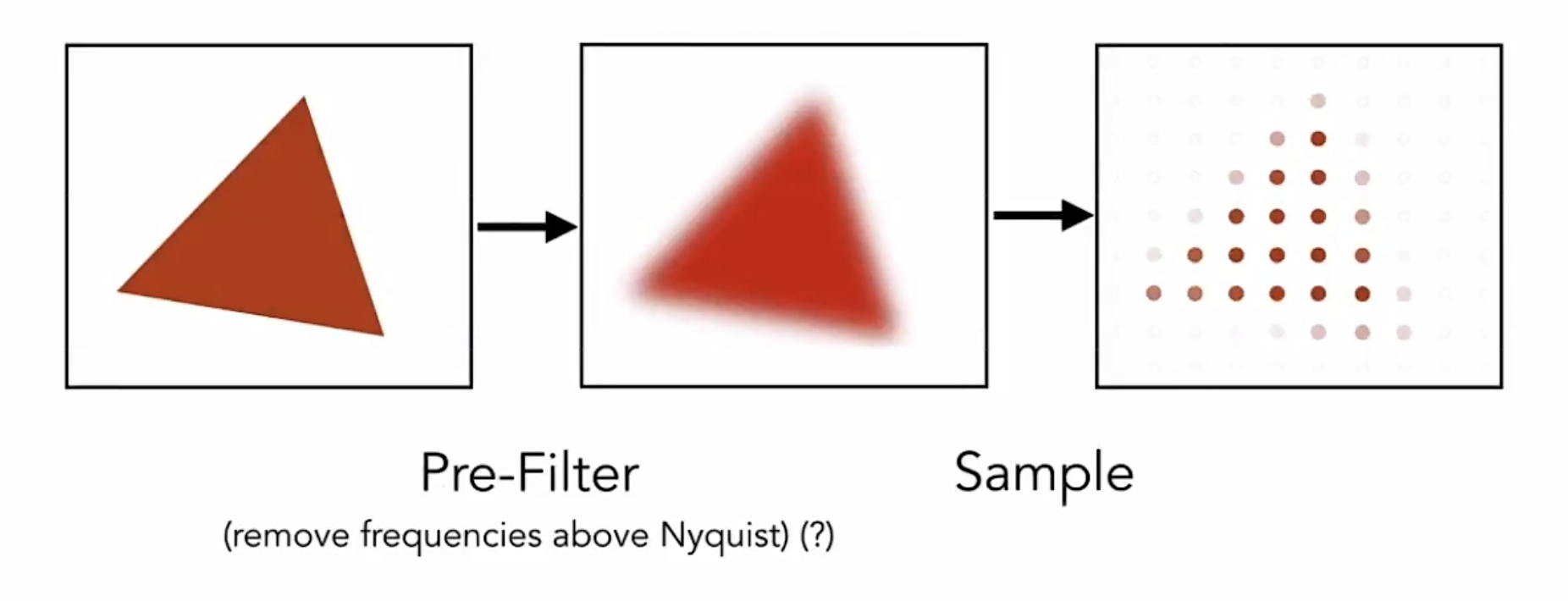
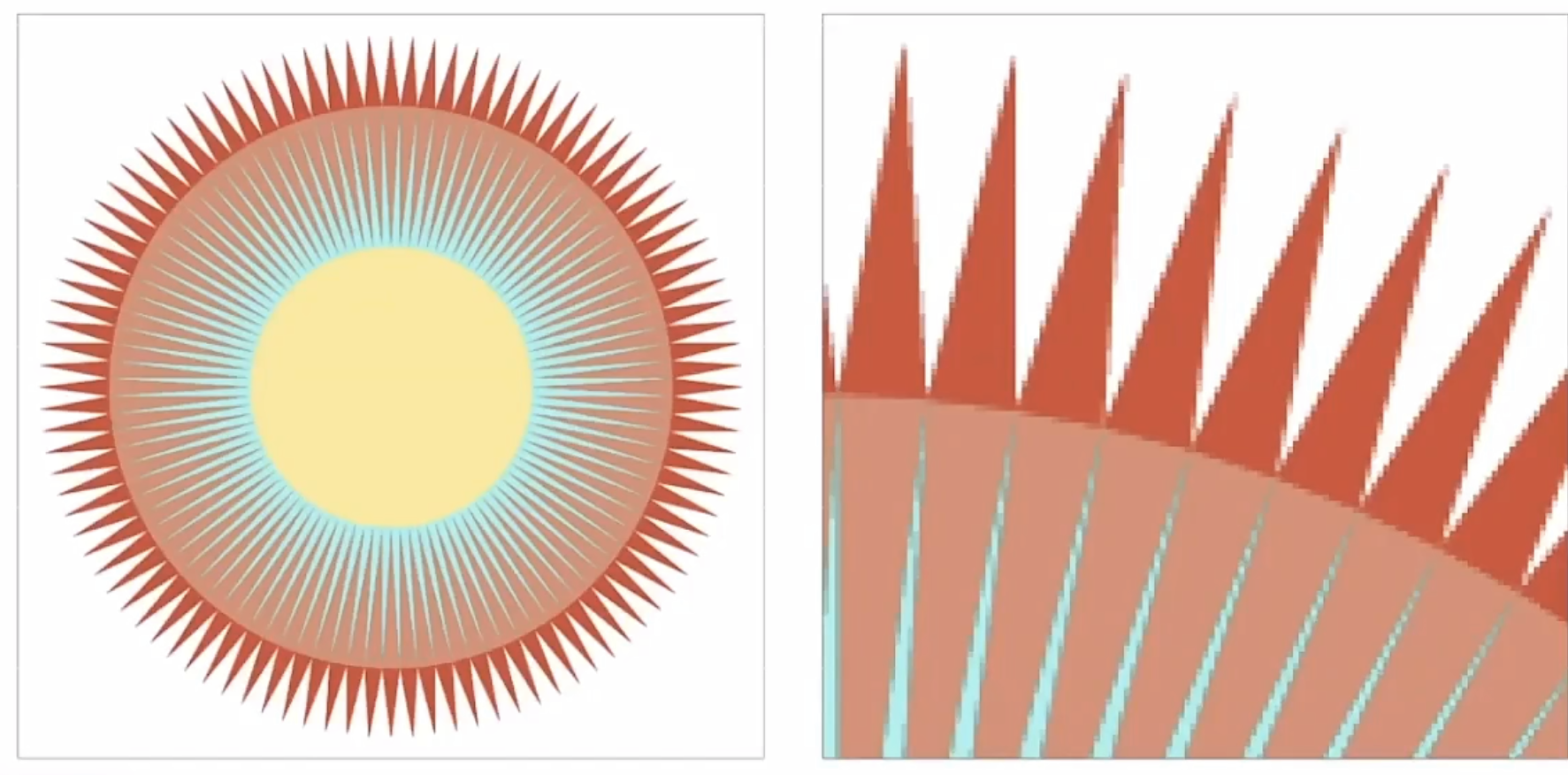
就像像素画中的人工抗锯齿,或者反过来

• Frequency Domain

  调整cos或者sin中自变量前面的系数,我们可以得到不同频率的波

  我们可以用傅里叶级数变换将一个函数变换为另一个函数,且可逆

  任何一个函数可以用傅里叶级数展开分解

  如果我们对两种截然不同的函数用同一种采样方式采样,得到的结果可能是相同的

• Filtering = Getting rid of certain frequency contents = Convolution (= Averaging)

• 高通滤波:只剩下高频信息//低通滤波同理

• 卷积定理:Convolutio in the spatiall domain is quual to multiplication in the frequency domain, and vice versa

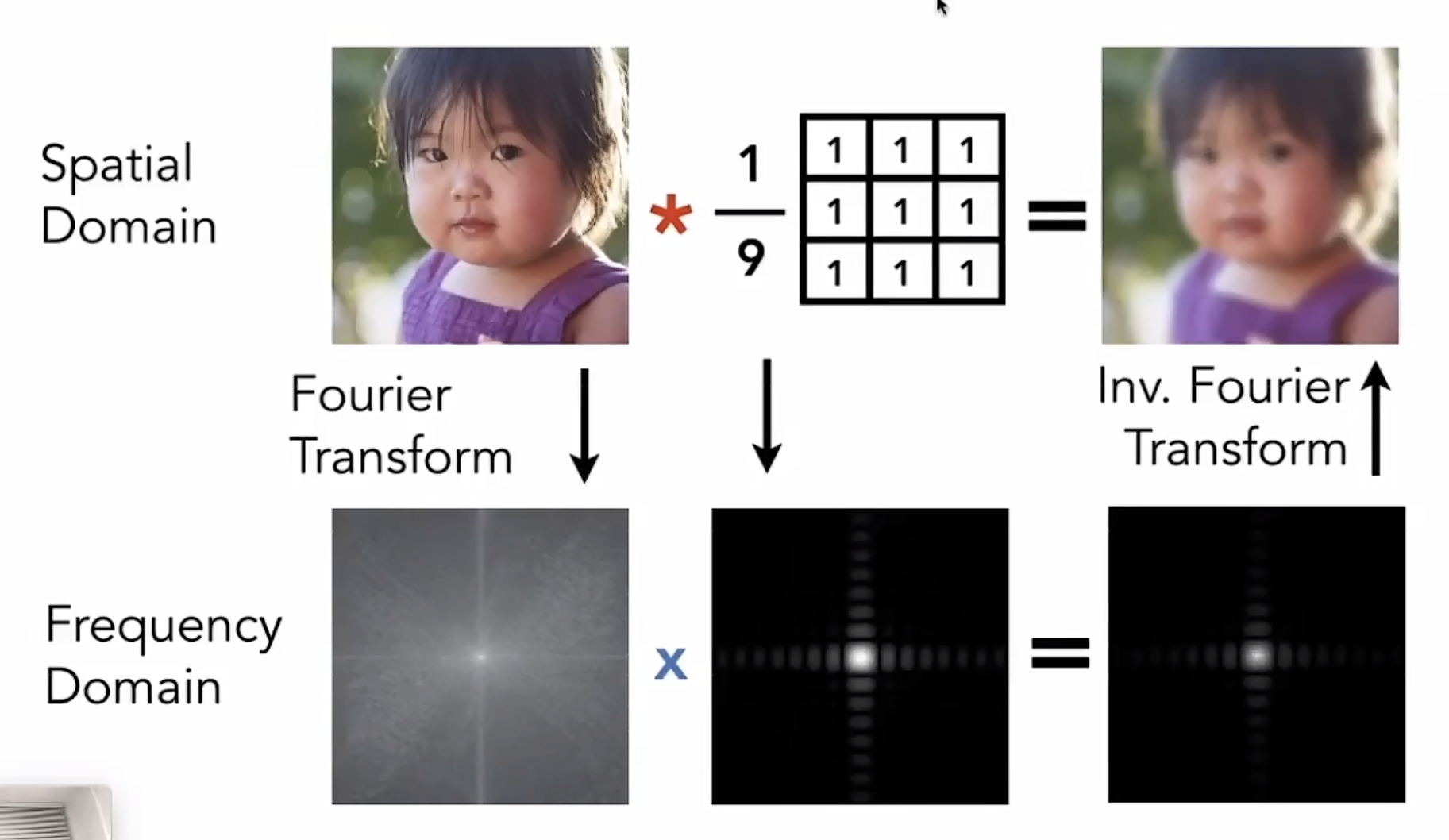
• Sampling = Repeating Frequency Contents

• 反走样的办法

1. 增加采样率。但这不是反走样要做的事情
2. Antialiasing先做模糊，再做采样。也就是先把图像的高频信息去掉，再采样。

实际中，用反走样的近似方法（MSAA），用更多的像素点去采样

为了减少计算的像素，可以用像素不规则分布或是像素复用

3. FXAA（Fast Approximate AA)
4. TAA(Temporal AA):将MSAA的样本引入到时间上

Lecture 7:Shading 1(lllumination,Shading and Graphics Pipelne)

可见性:如果我们要把一堆物体放到屏幕上，一定有顺序。由远及近

画家算法：先将远处的东西做光栅化，再将近处的东西做光栅化

但有些情况相当复杂：

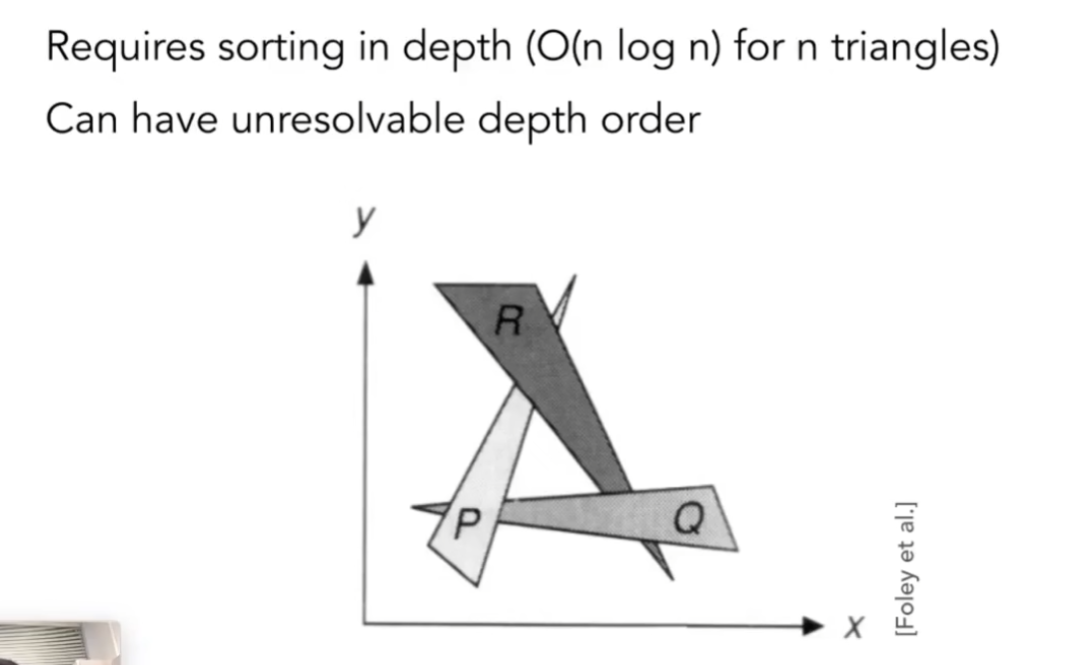
此时我们无法定义图形的深度关系

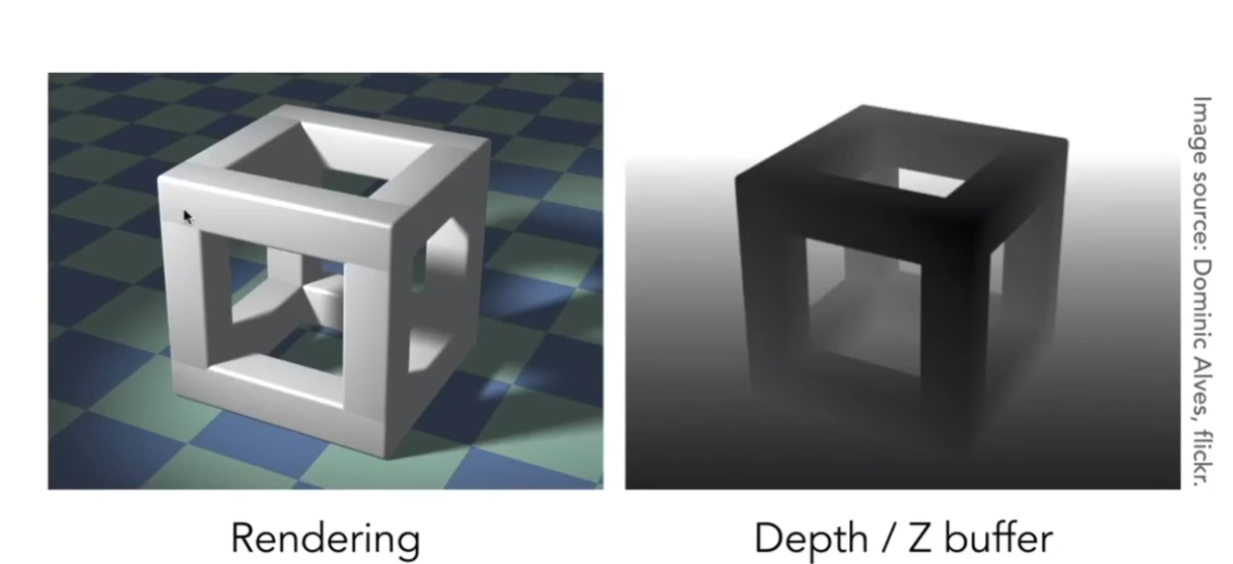
Z-Buffer

Z-Buffer(深度缓存)：记录像素，而不是图形的深度

在渲染时，我们既记录图形的深度，也记录像素的最近深度

如果发现某个像素的最近深度比它的之前的图形离屏幕更近,更新这个像素的深度

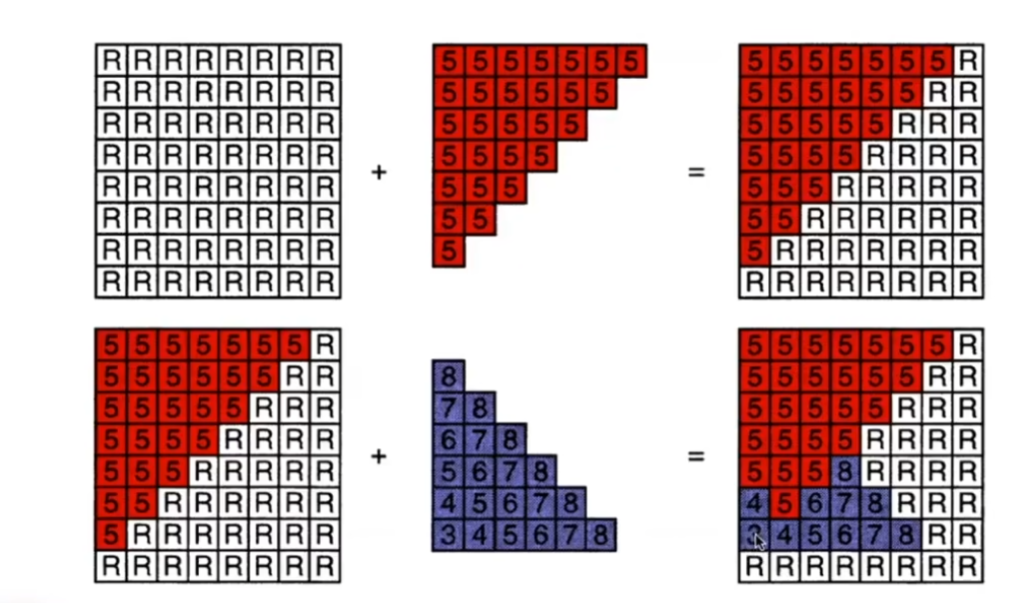
深度缓存的结果与渲染顺序没有关系

Shading

着色：The processo of applying a material to an object.

• Shadig is Loval

着色只考虑这个点自己

Blinn-Phong refectance model

对于一个点光源,对于某个时刻发出的光,它的能量在每个时刻都应该在一个球壳上,且球壳越来越大,单位球壳的能量越来越小

从式子可以看出,漫反射的反射方向v不记入计算.也就是说,从任何方向看到漫反射的物体,获得的能量都一样

Lecture 8 Shading2(Shading ,Pipeline and Texture Mapping)

如果物体不是那么光滑,镜面反射的方向会适当发散

当我们观察方向和镜面反射的方向接近的时候,我们就看到了高光

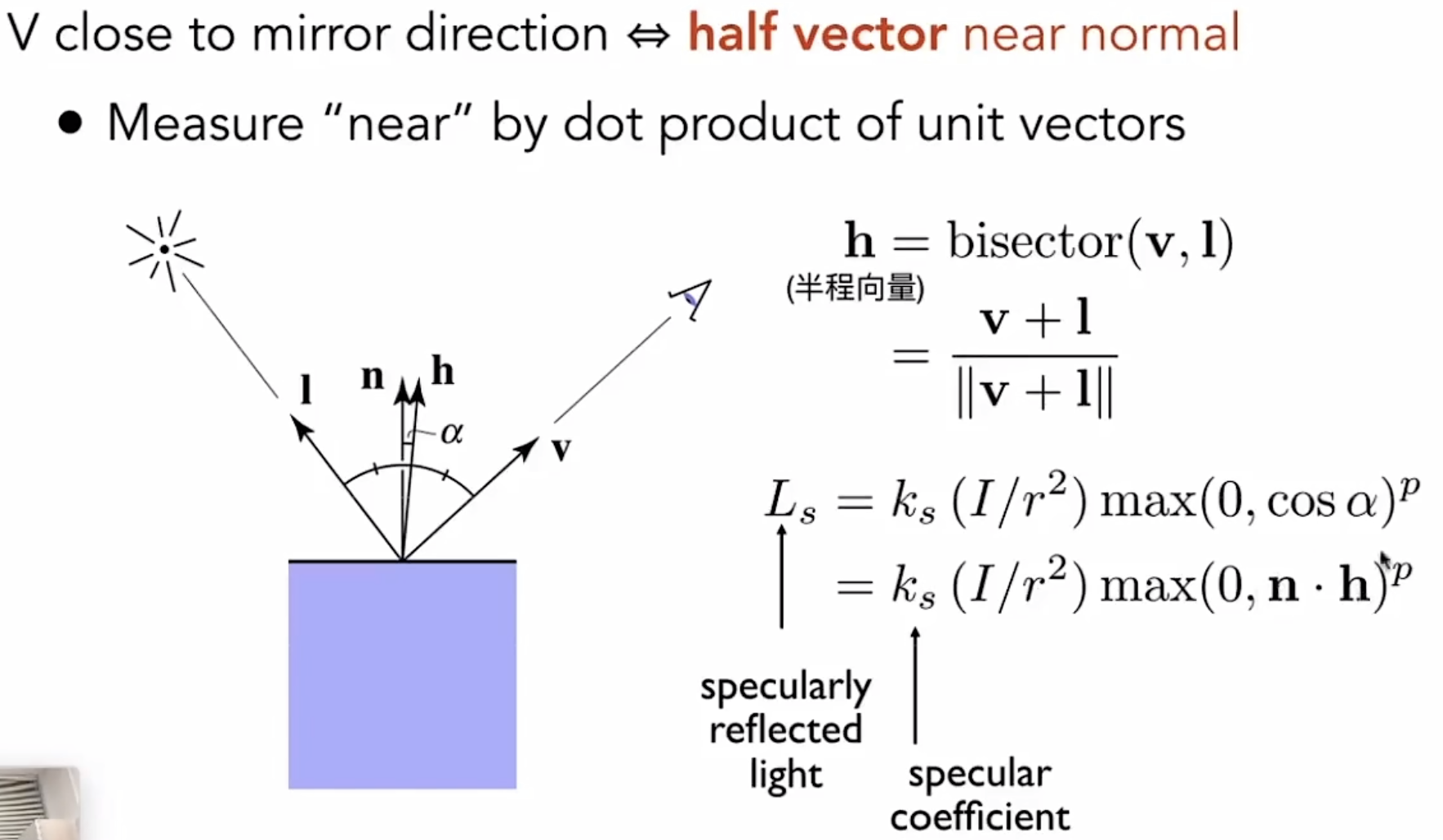
将环境光项,漫反射项,高光项相加,得到Blinn-Phong reflection Model

Shading Frequencies(着色频率)

Flat shading:Triangle face is flat -one normal vertor , Not good for smooth surfaces

Gouraud shading :对每一个顶点着色

Phong shading : 对每一个像素着色

当几何面足够复杂的时候,可以选用较低的着色频率

如何计算顶点的法线:相邻面的法线求加权平均

Graphics Pipeline

把所有这些东西加一起,称作Graphics Pipeline

决定这个过程的代码叫shader

Shader Programs

OpenGL是图形学的API,可以用来写shader

uniform sampler 2D myTexture;
uniform vec3 lightDir;
varying vec2 uv;
varying vec3 norm;

void diffuseShader()
{
    vec3 kd;
    kd = texture2d(myTexture,uv);
    kd*= clamp(dot(-lightDir,norm),0.0,1.0);
    gl_FragColor =- vec4(kd,1.0);
}

推荐网站:shadertoy.com

Texture Mapping(纹理映射)

如何定义一个点的基本属性?

首先,把属性定义在表面上.

任何一个三维物体的表面都是二维物体

纹理,就是一张图,可以蒙在一个三维物体的表面

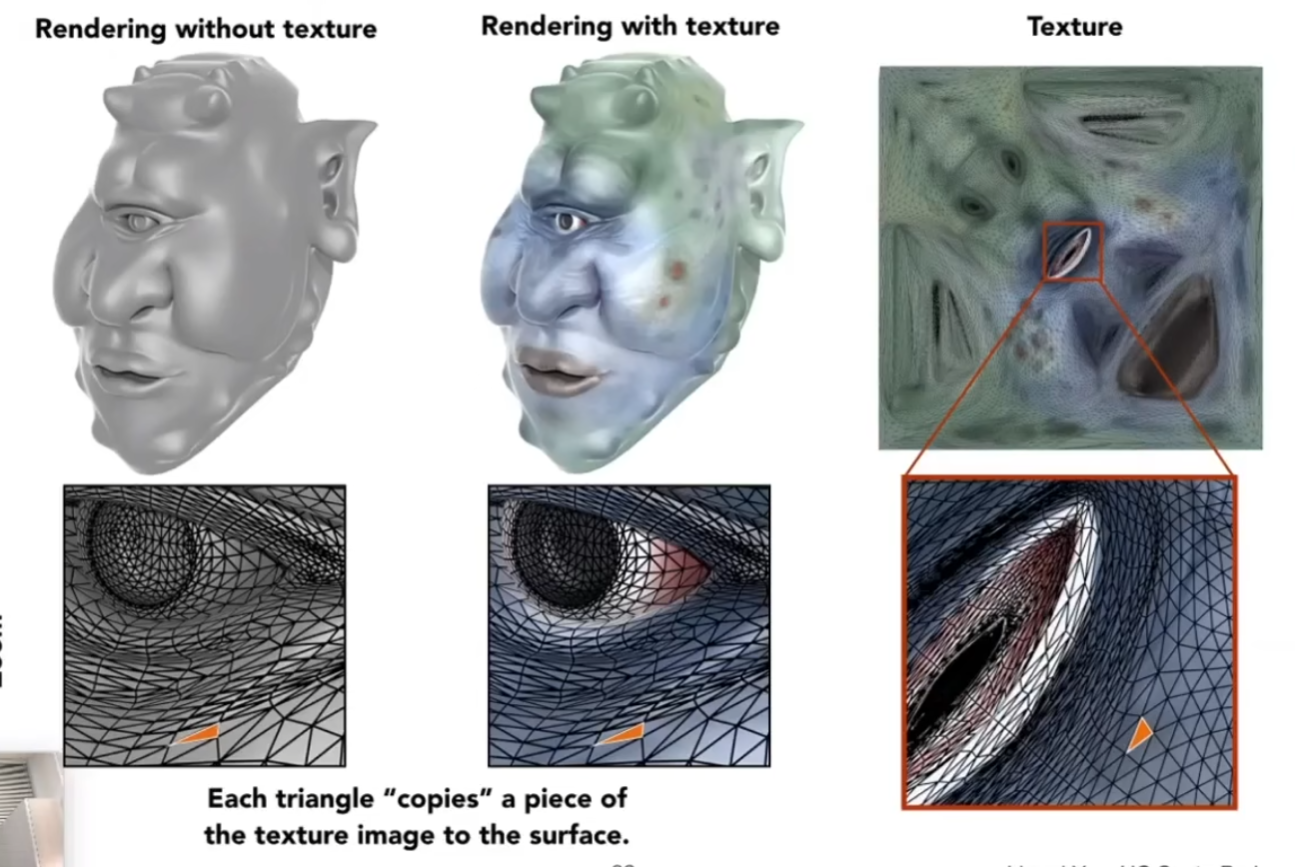
怎么把一个空间的表面映射到三角形上,我们不管,假设已经有了这种映射

现在在纹理上定义坐标系(u,v),

Lecture 09 Shading(Texture Mapping Cont)

有时我们希望在三角形内部插值某种属性,得到一个平滑的过渡

完成这个操作,我们需要重心坐标

以及,我们已经知道,模型上的一个三角形映射到了纹理上的一个三角型,但三角形的内部,我们也可以用插值计算纹理映射到模型的颜色

重心坐标

定义

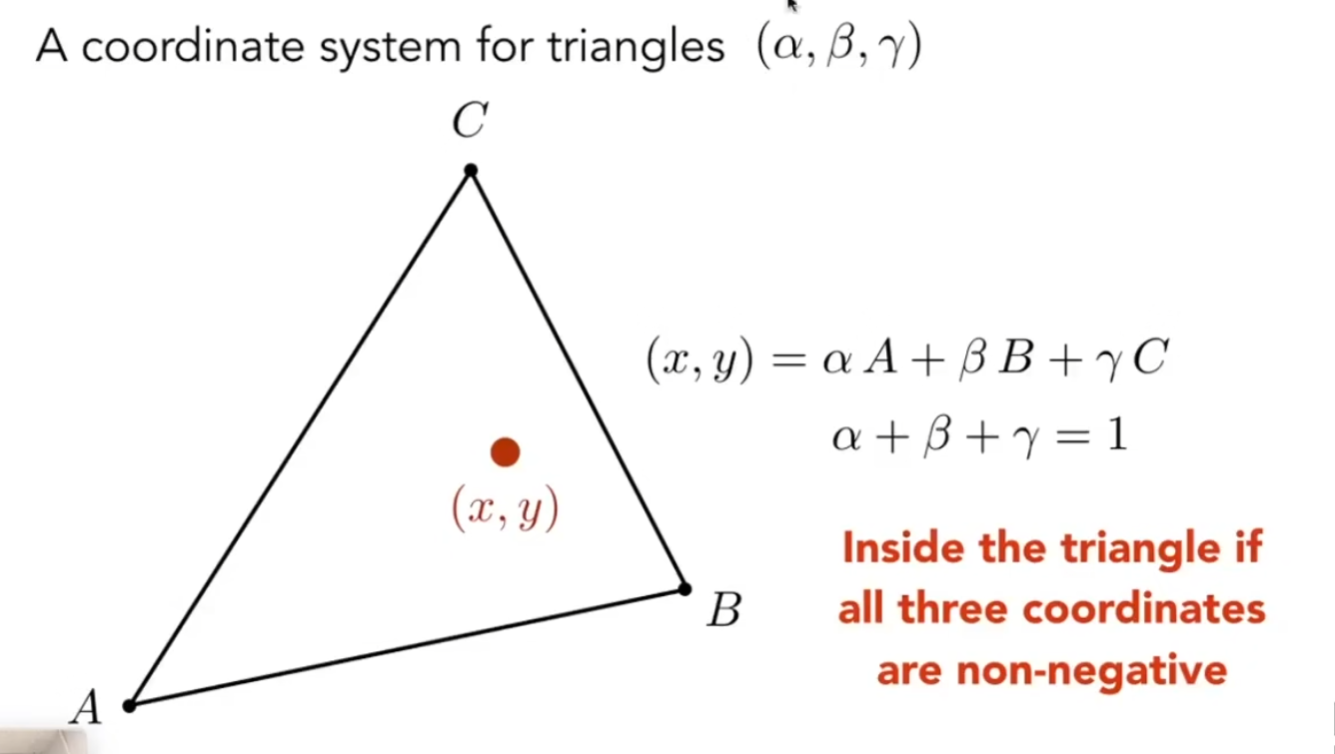
在三角形平面中一点的坐标,可以用三角形三个点坐标的线性组合表示,如果αβγ都是非负的,说明重心坐标在三角形内部

αβγ可以用面积比来得出

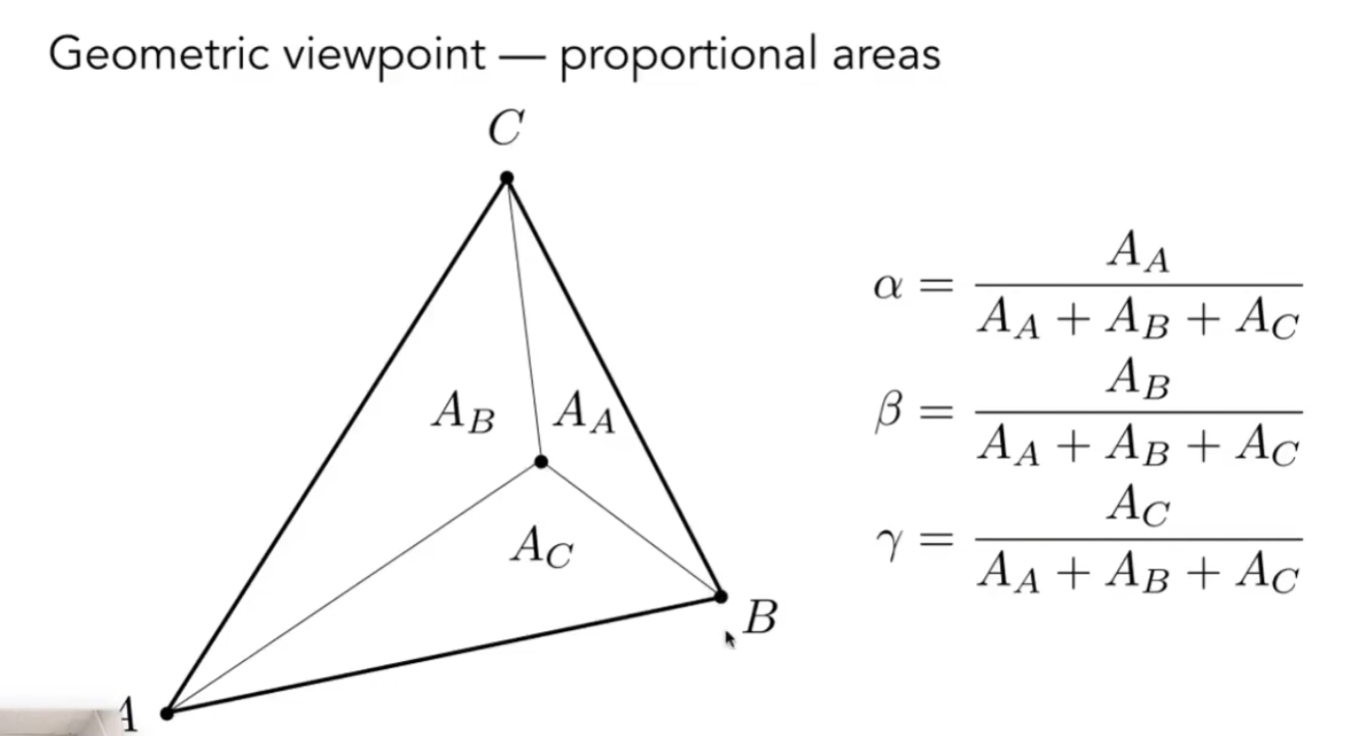
或者

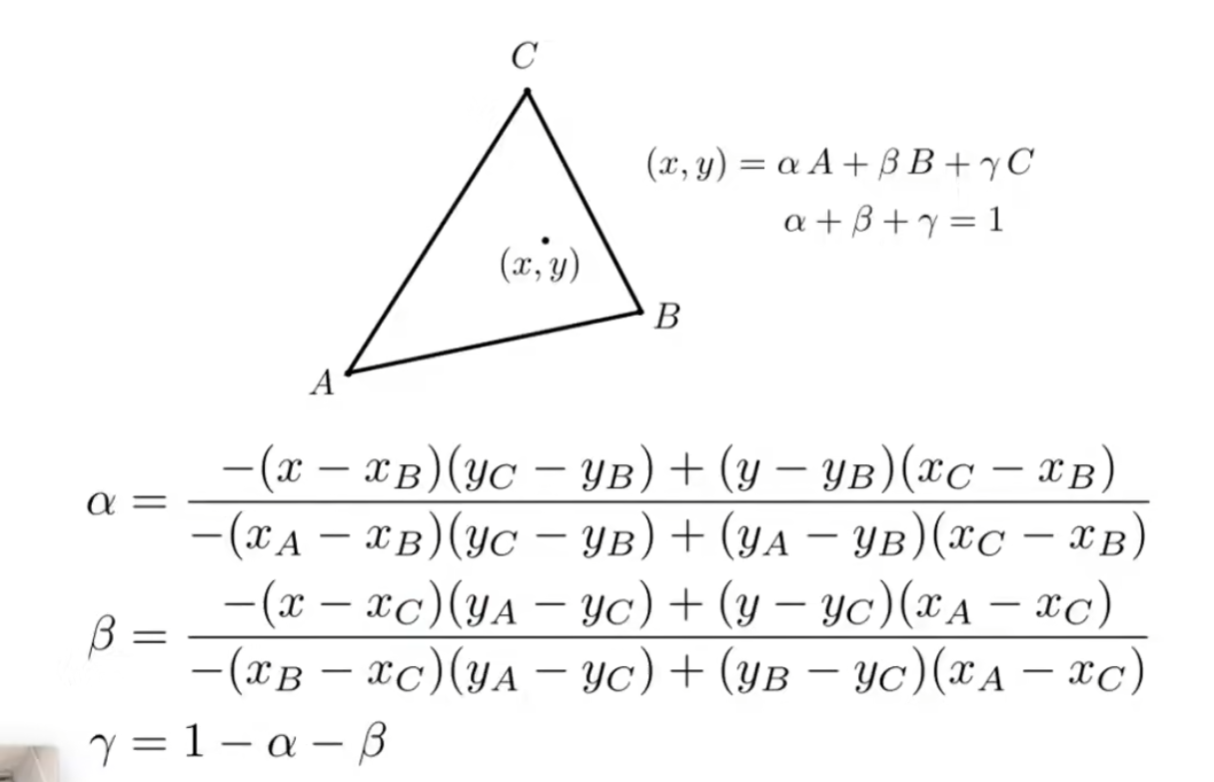
现在,得到了任一点的重心坐标,我们就可以使用重心坐标来计算三角形中任意一个点的插值,下图为颜色插值

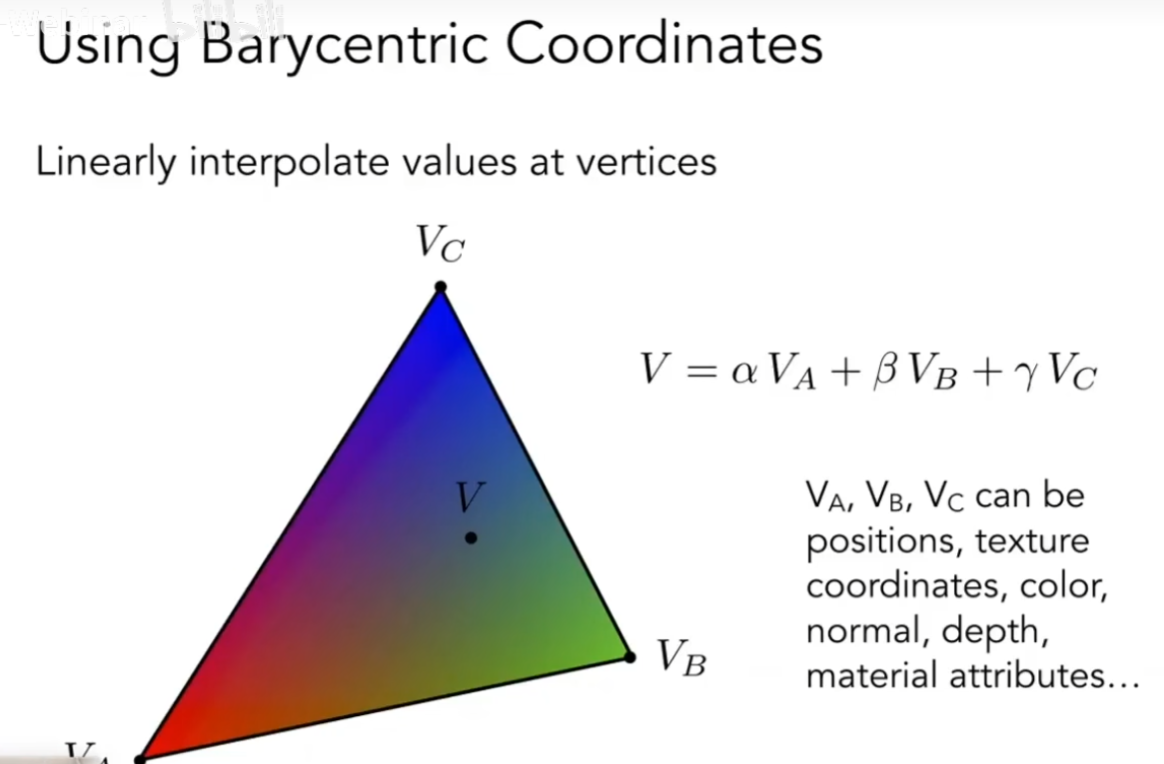
• 重心坐标无法做到投影下不变

应用纹理

我们可以直接用纹理代替漫反射光的颜色,就相当于是将图贴在这个模型上了

至于一个片元用纹理上的哪个点,就是纹理映射的事情了

纹理的放大：如果纹理太小了怎么办

如果纹理太小，屏幕的分辨率太高，一些点会映射纹理的同一像素

Bilinear interpolation

线性插值: lerp(x,v0,v1) = v0 +x(v1-v0)

计算某一个点的水平和竖直插值

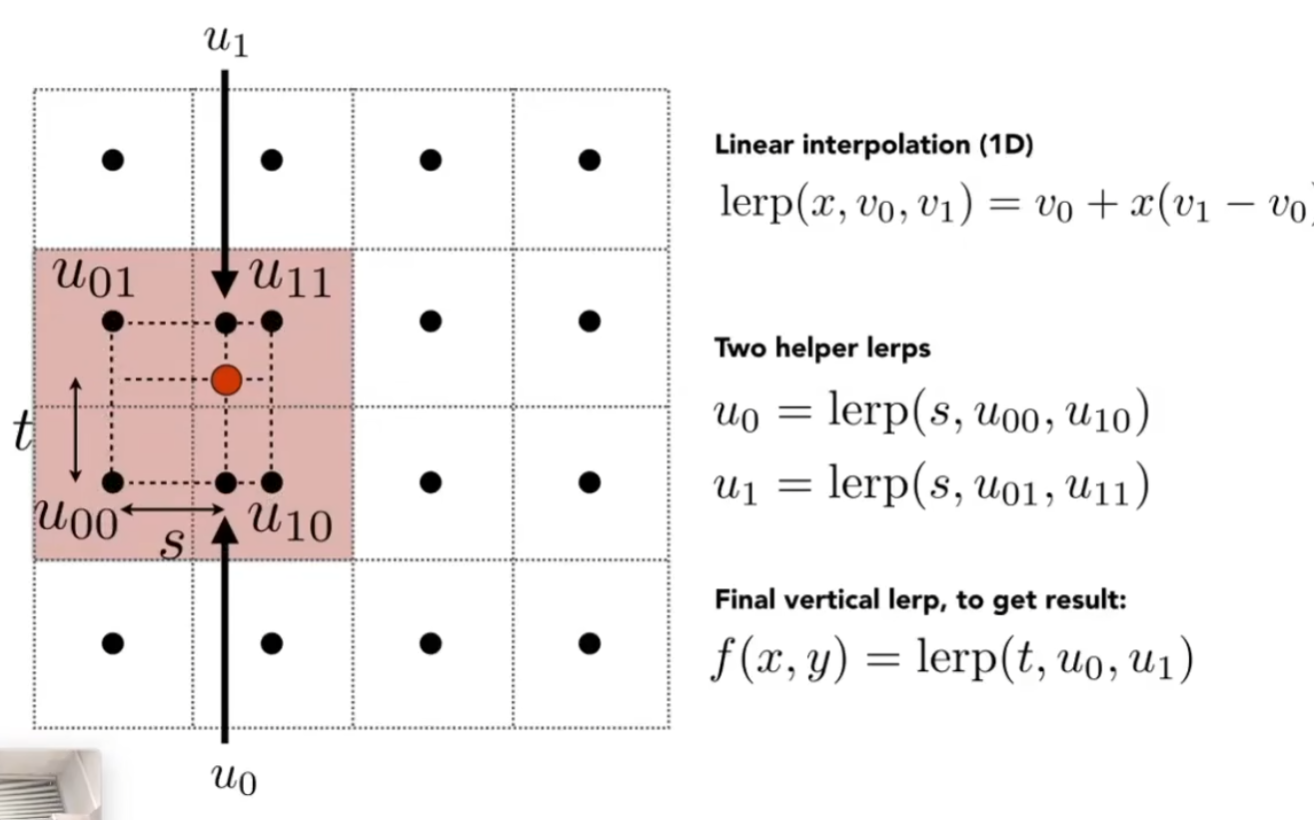
这样我们可以得到点与点之间的平滑过渡

如果纹理太大了会怎么样

如果纹理太大,反而会引起更严重的问题:走样

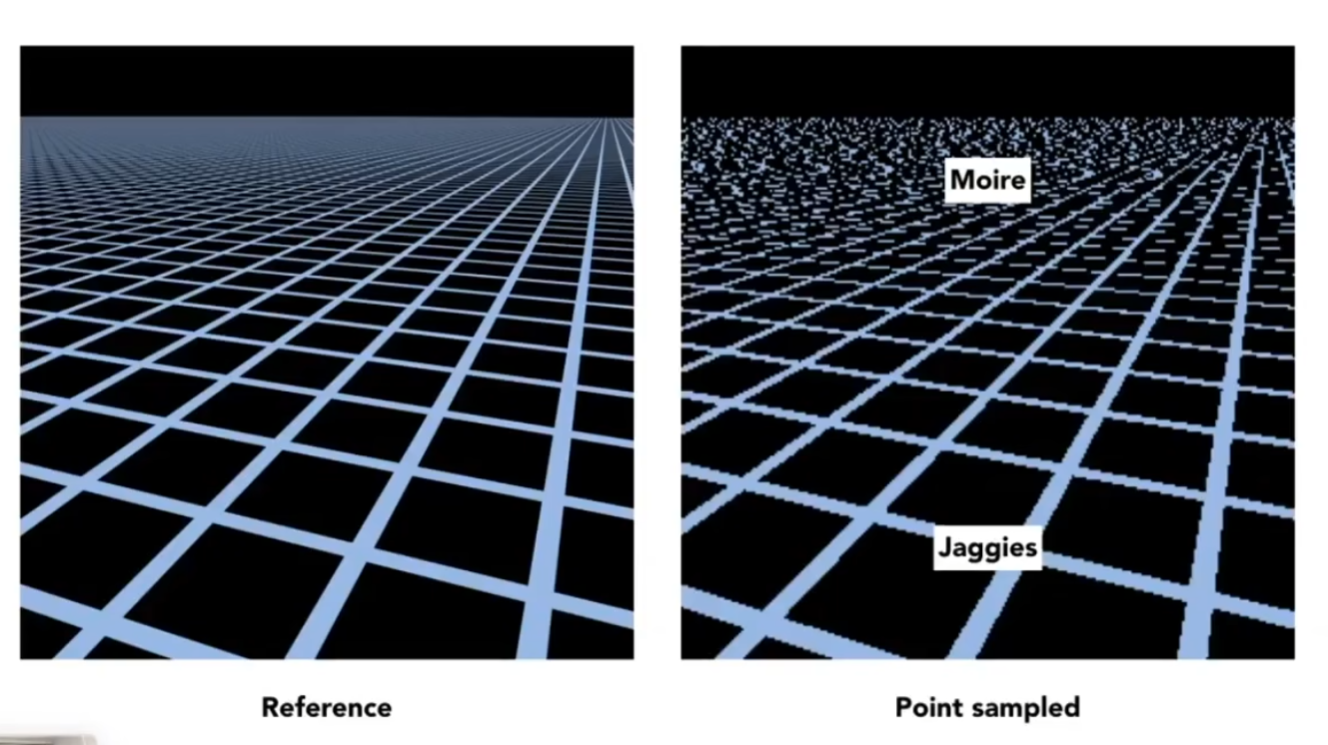
如果纹理过大，屏幕上一个像素覆盖的纹理上的区域过大，如果此时取这个区域的平均值作为屏幕上像素的值，走样就出现了

在这个情况下走样的原因：在一个像素内的采样频率较低

解决办法：避免采样
如果我们可以立刻知道一个区域内的平均值，而不使用采样，就可以避免低频采样的问题

Range Query

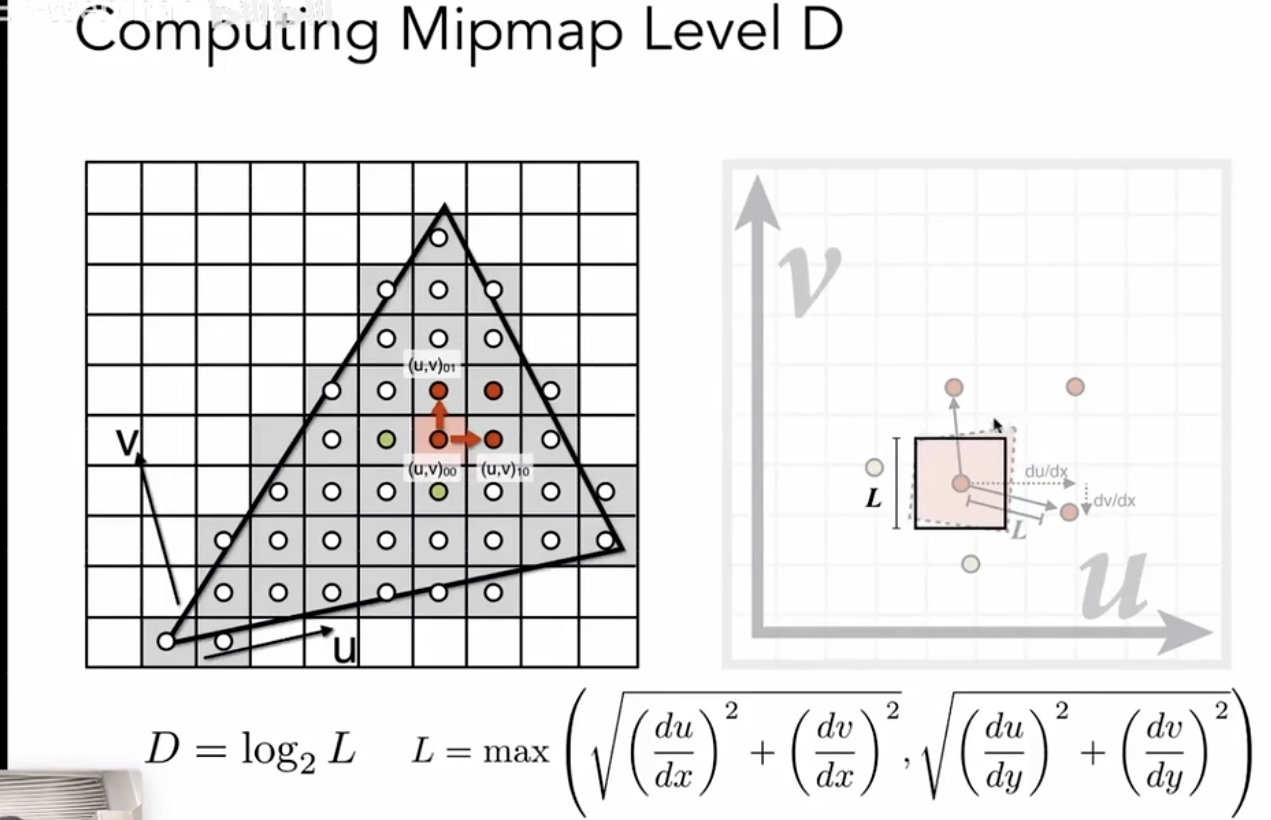
不同的物体有不同的像素覆盖的大小，此时我们就需要范围查询

Mipmap

Mipmap允许近似的正方形的范围查询
我们拿到了一个纹理之后，先生成纹理里的mipmap，也就是分别生成它在不同大小下（不同层）的复制体

使用mipmap

任何一个像素都一个纹理上的区域，那么我们也能知道一个像素映射的纹理区域占的长度，也就是区域的大小
这样我们就可以动态的查询一个物体所需的mipmap的层数
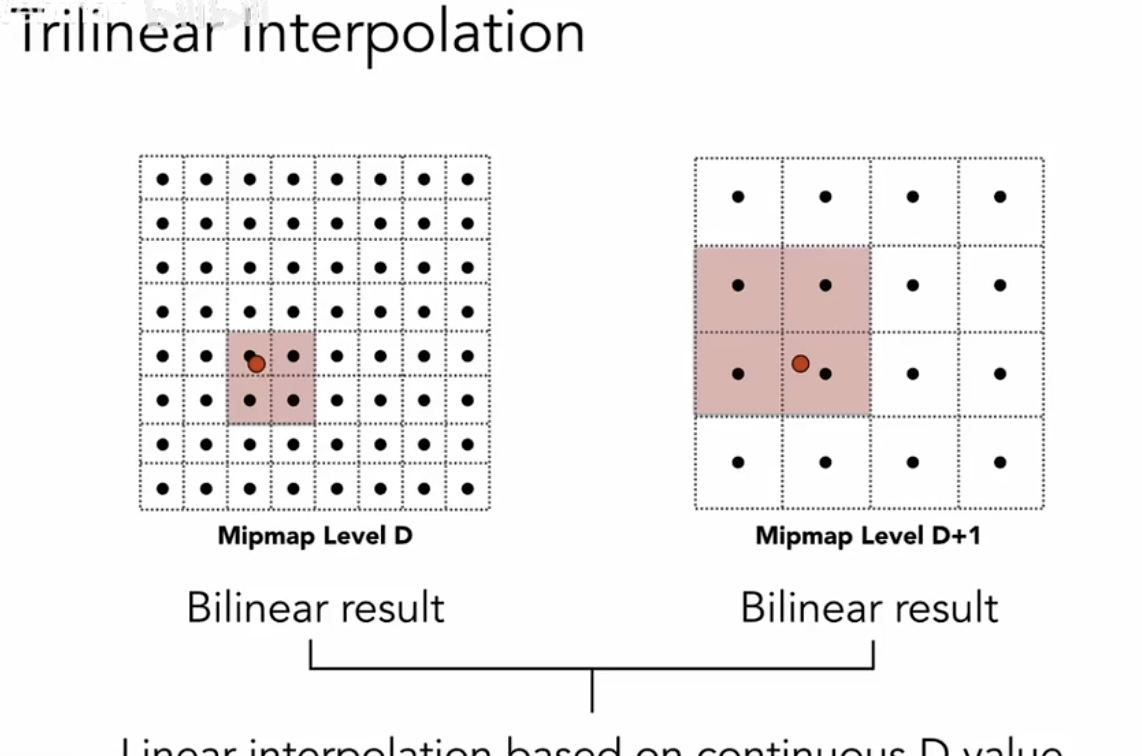
如果一个像素映射的区域不大不小，我们又可以在两个mipmap层间插值（Trilinear Interpolation）

Mipmap的问题

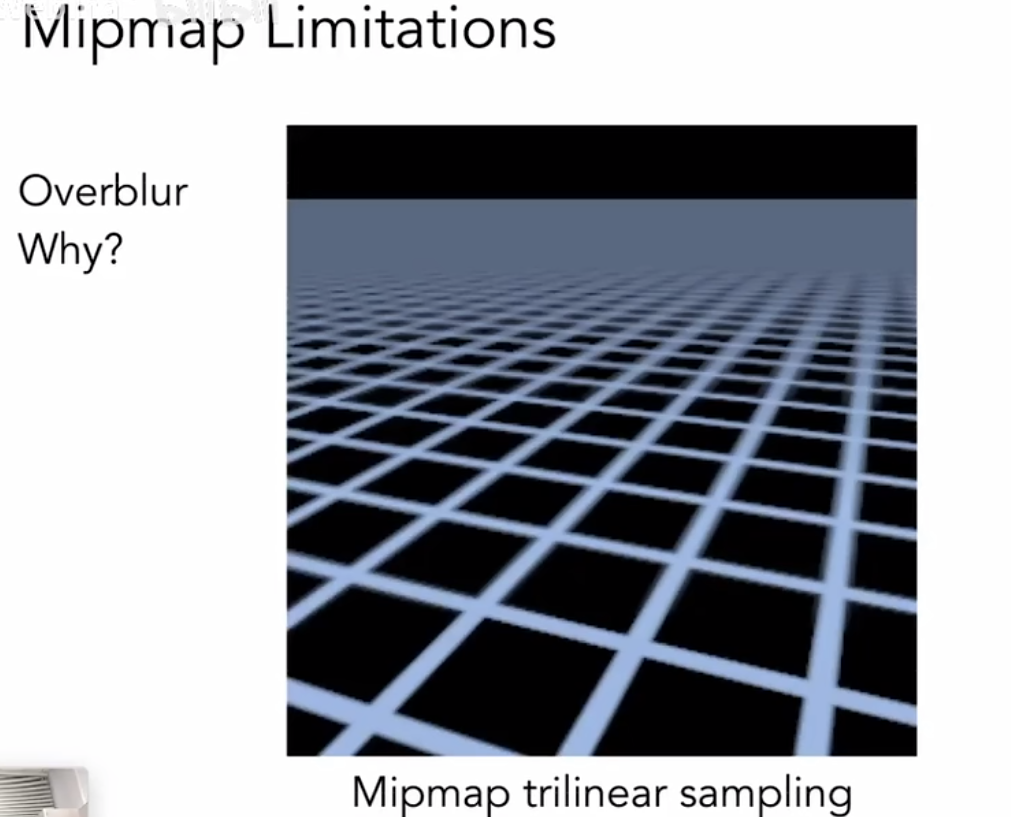
mipmap会使远处的东西糊掉，也就是（overblur）

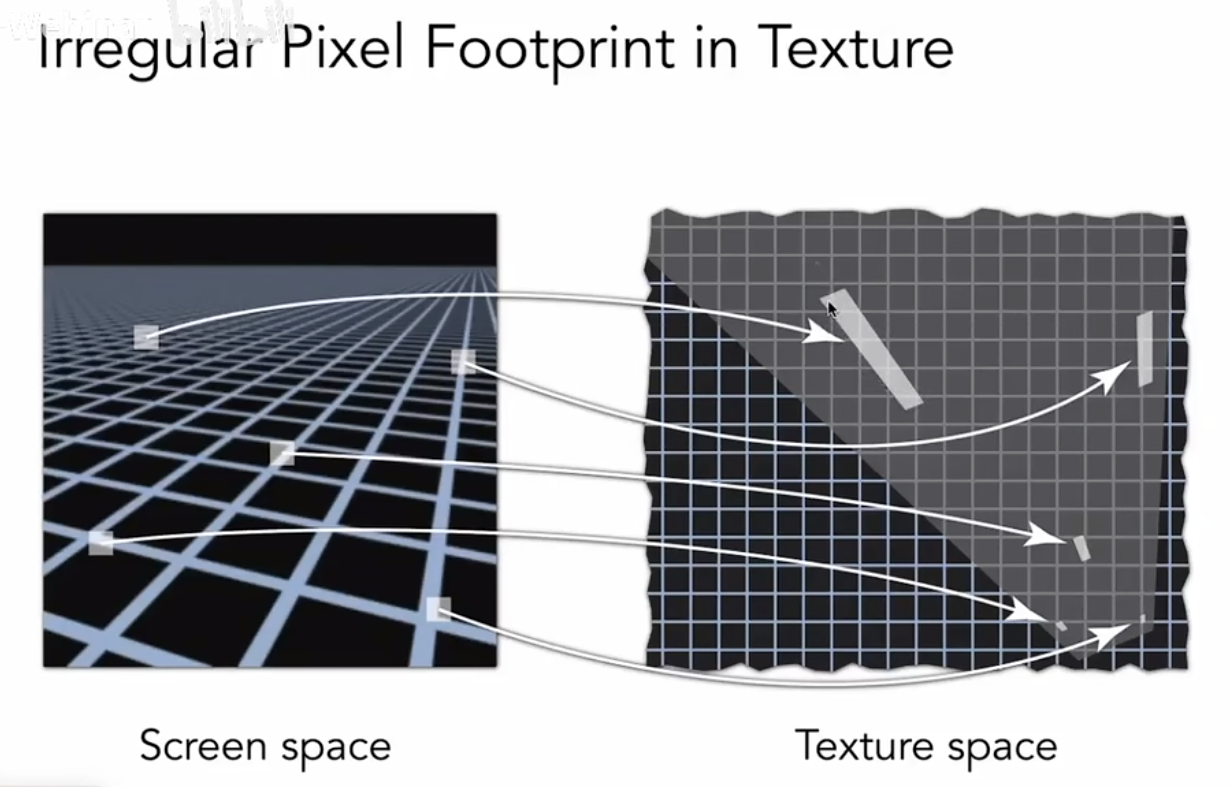
一个部分解决三线性插值的问题：各向异性过滤
屏幕上的像素映射到纹理上，不一定是一个规则的区域，使用各向异性过滤，以允许我们在一个矩形区域上查询，但不能完全解决其他形状的问题

Lecture 10:Geometry 1(Intrdouction)

环境光照(Environment Map)：如果我们可以把各个方向进入人眼的光记录下来,这就是环境光照

Spherical Environment Map:我们可以假设我们有一个光滑的球,那么我们就可以用这个球记录环境光

但Spherical Map有一些问题,当球记录靠近地球极点位置的环境光,展开后会出现画面扭曲

解决方案,我们可以用一个立方体记录环境光

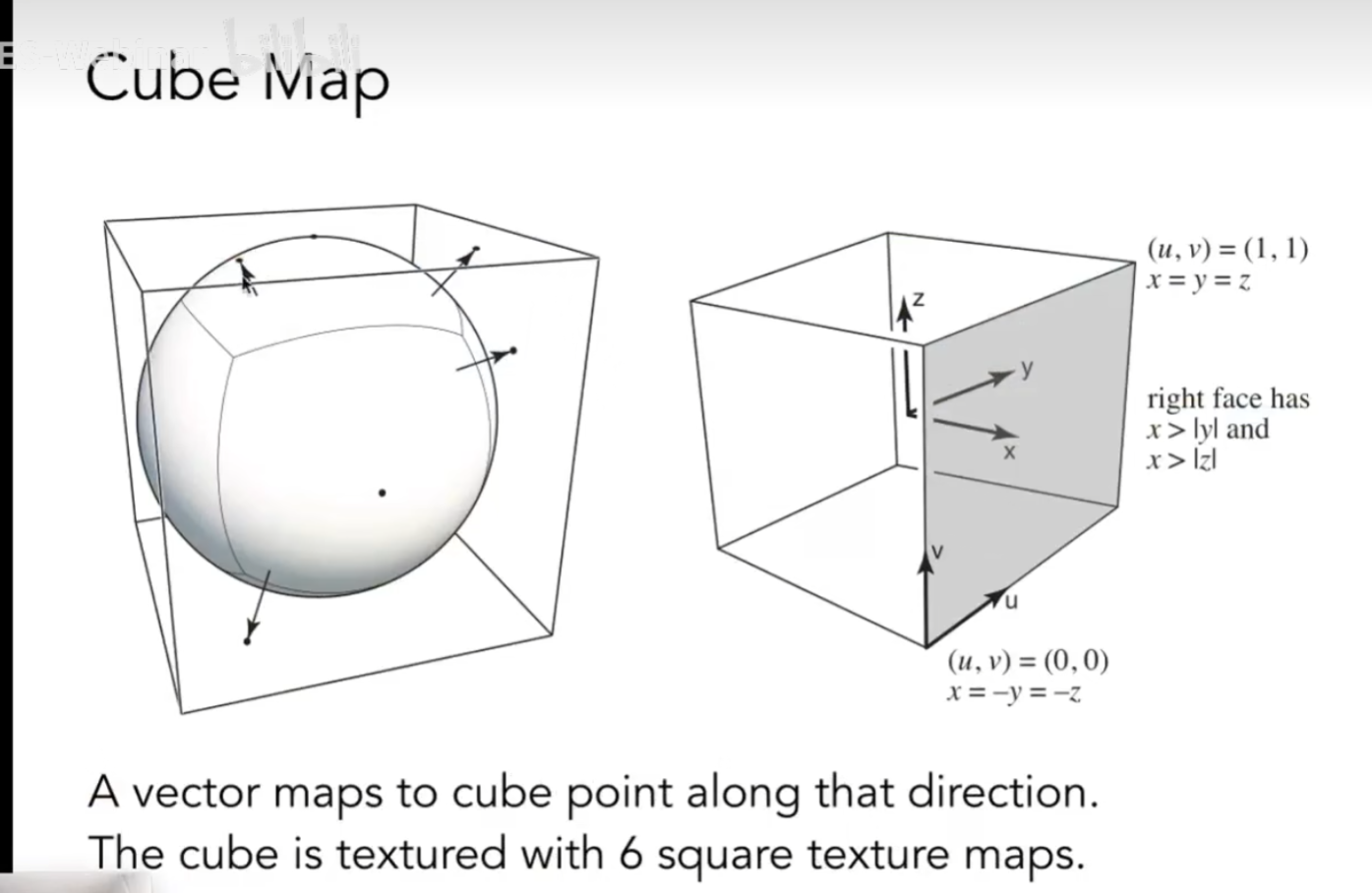
纹理可以应用于凹凸贴图

我们可以定义在一个表面上,每一个点的相对高度

如果想表示一个橘子,我们需要的三角形太多了,但我们也可以不用三角形,只定义表面每个点的相对高度,即可出现凹凸形的着色对比

如何定义相对高度

我们对像素的法线作扰动

计算法线

可以计算一个曲线的导数,作与曲线切线垂直的射线,即可得到法线

或者,我们可以定义一个局部的坐标系,在这个坐标系里认为原法线是(0,0,1),用纹理映射的办法修改法线坐标,再将坐标系转换回世界坐标

凹凸贴图没有像位移贴图一样改变定点的坐标,有一定的局限

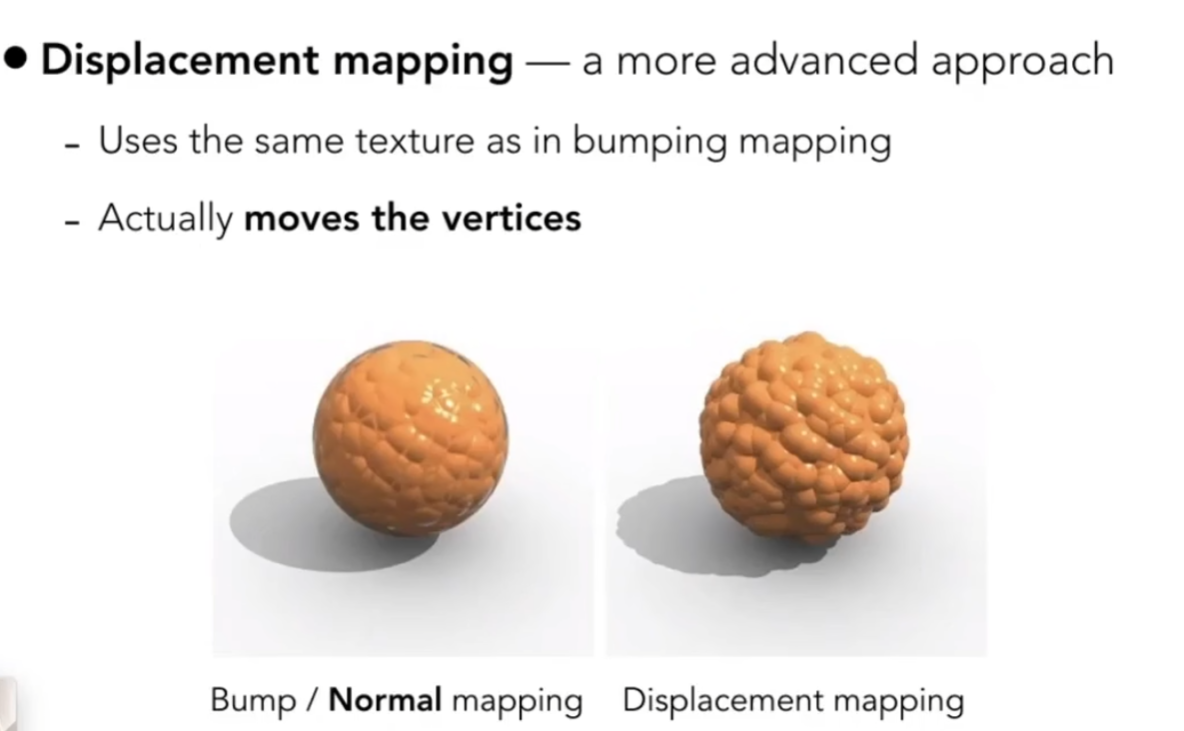
几何的表示方法

隐式几何

概念：不会告诉你几何的点在哪，而是告诉你几何中点点关系
比如，圆的标准式

隐式几何的缺点：很难直接确定几何的点在哪
好处：很好判断一个点是否在一个图形上

相对的也有显示的表达方法

显示几何

通过参数映射的方法表示

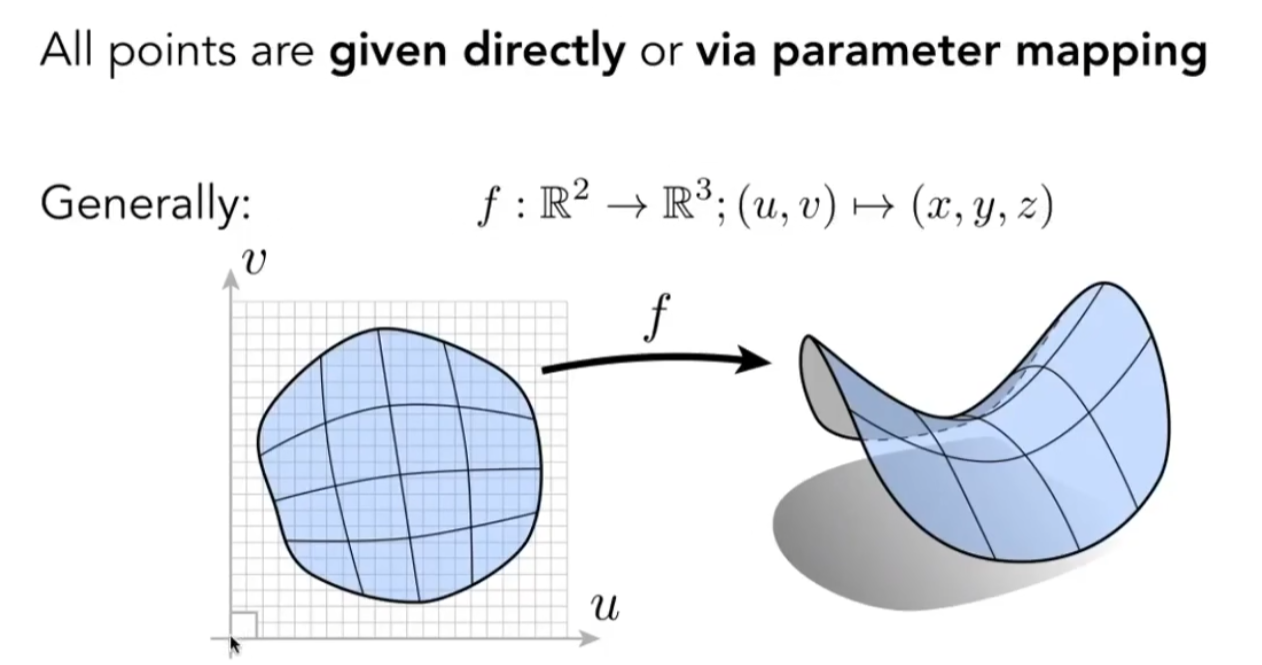
我们需要判断在什么情况下使用什么表示方法

CSG

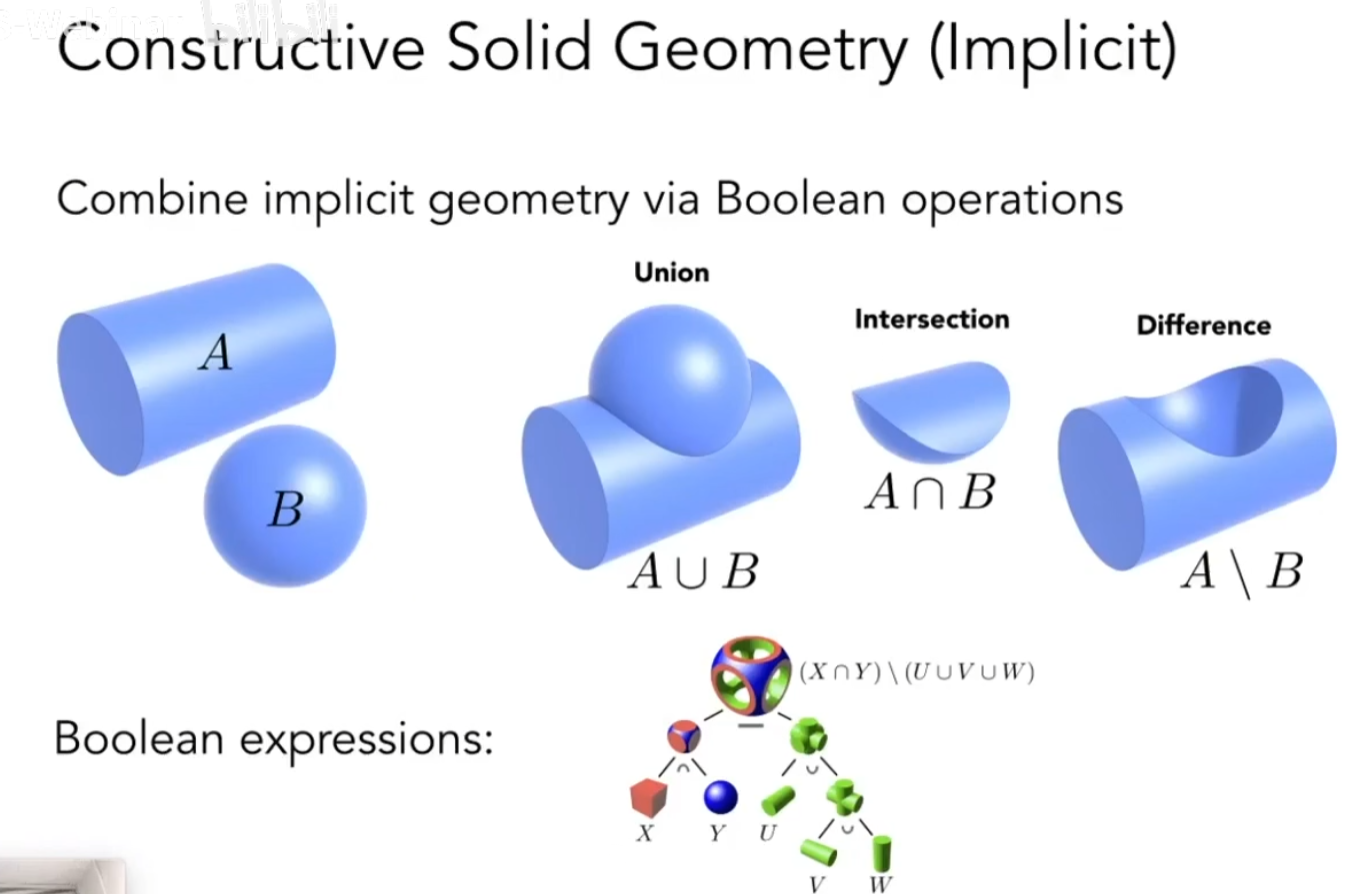
通过几何之间的交并补等,可以用简单的几何表示复杂的几何

距离函数

我们描述一个几何的点到一个表面的最近距离,来隐式表示几何

通过距离函数融合几何

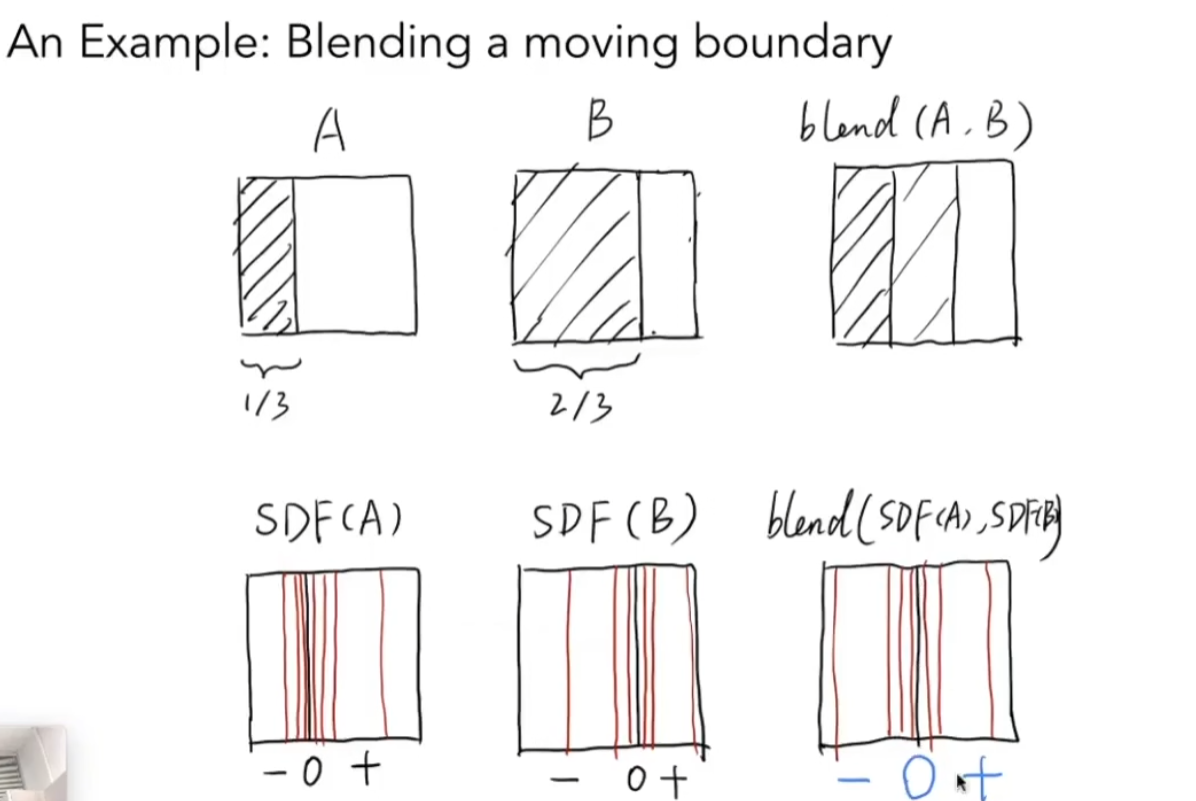
水平集

记录一个坐标系中,一个函数的值相同的点

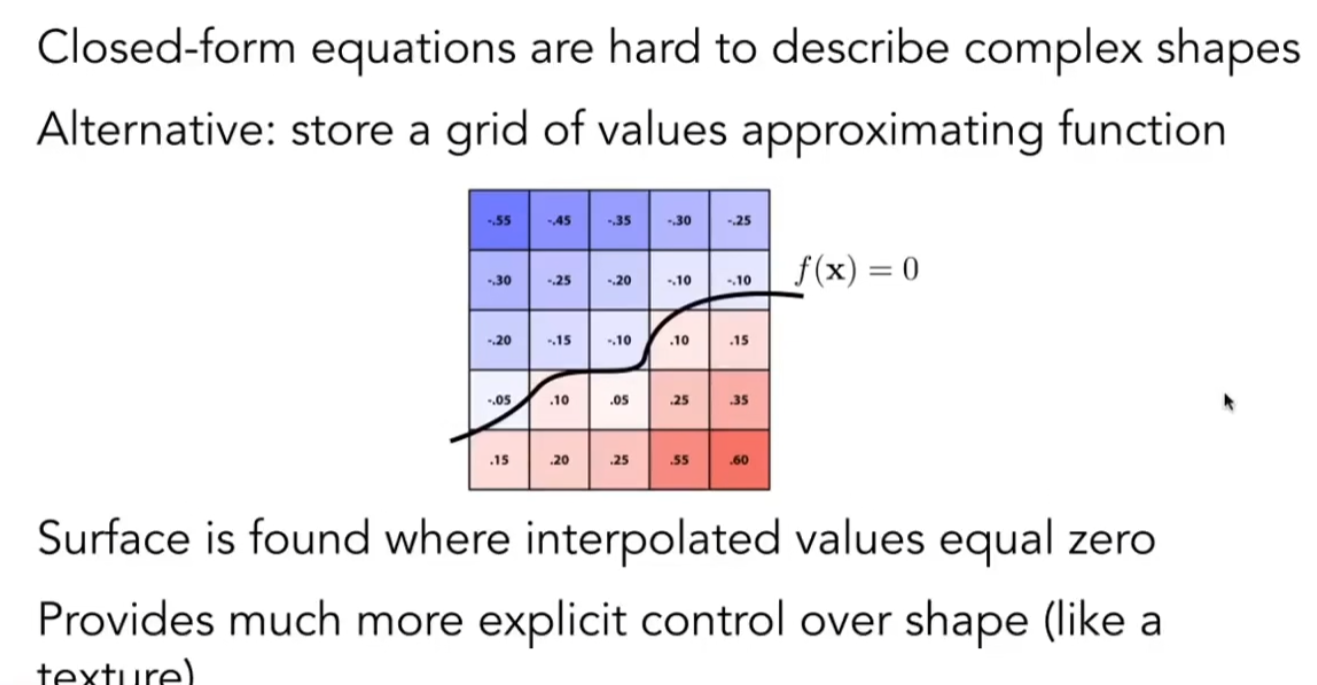
地理上的应用:等高线

我们也可以把水平集定义在三维空间中

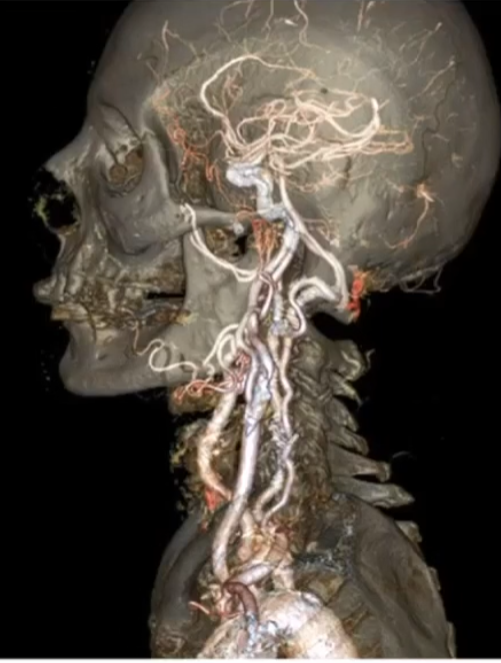
我们现在可以用距离函数水平集描述一个复杂几何的表面

Fractals(分形)

一个几何的图形在内部重复

这样类型的几何在渲染时很容易出现强烈的走样

Lecture11:Geometry 2(Curves and surfaces)

显示的几何也有许多不同的方法表示

显示几何

点云

我们不考虑一个物体的表面,而是考虑一个物体是由一堆点组成的,如果我们考虑的点足够细,足够密,点云就可以变成一个几何的面

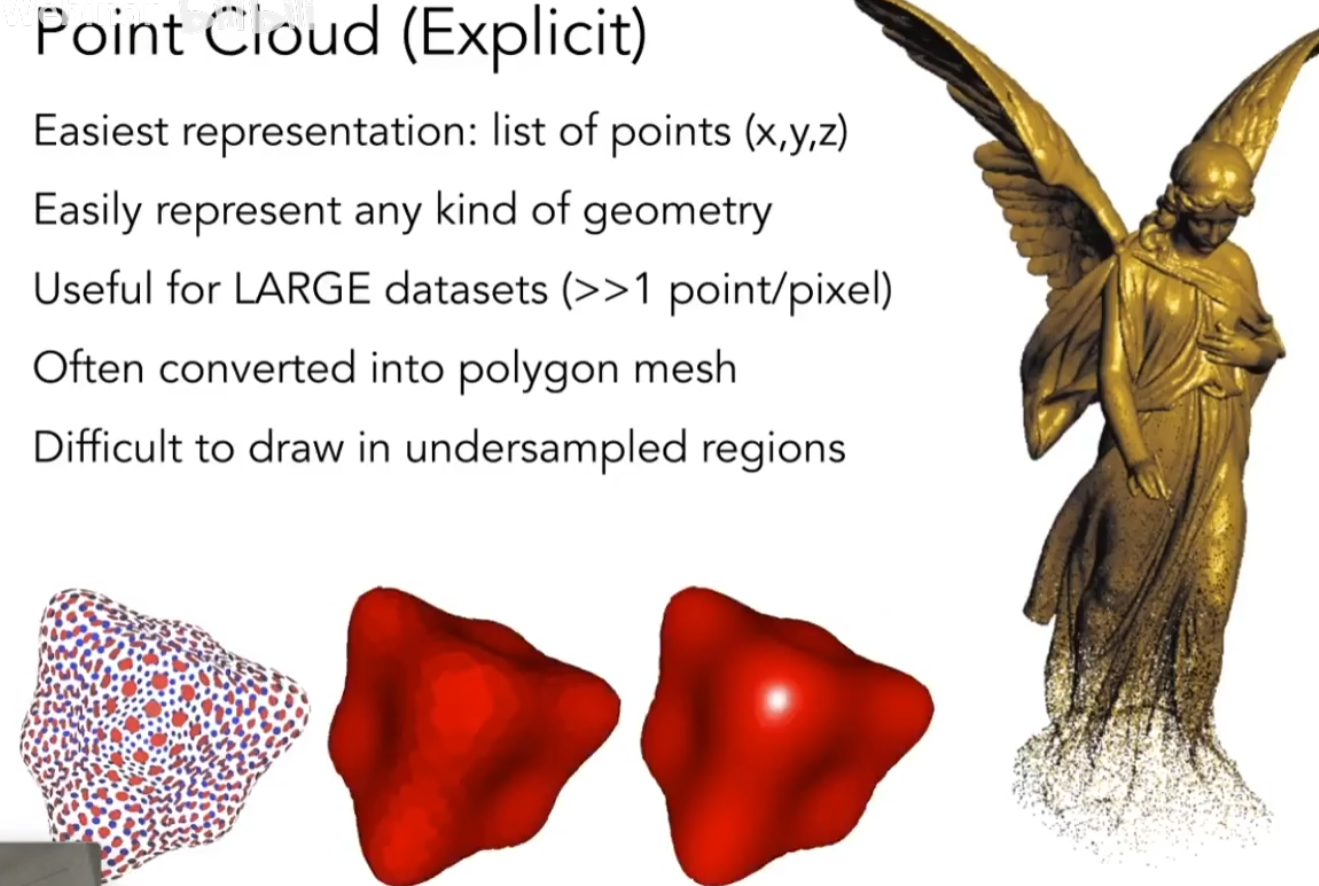
多边形面

任何一个面都可以拆成一堆小的三角形

我们可以通过定义很多三角形来描述一个几何

贝塞尔曲线

我们用一系列控制点定义一个曲线,且定义曲线的性质

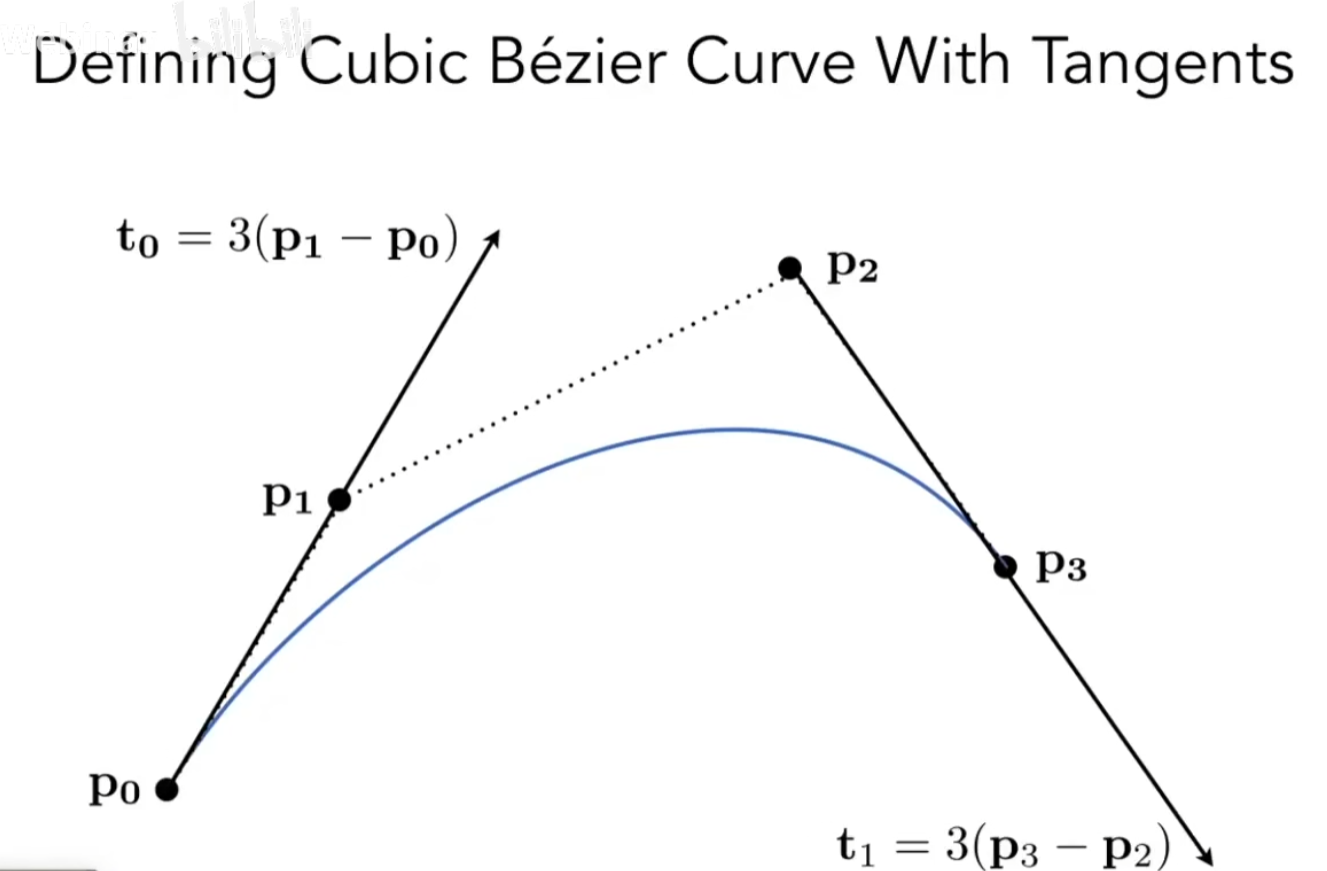
在四个控制点间连线,线段分半,继续分半,当每个线段只有一个点时,我们就得到了一个曲线

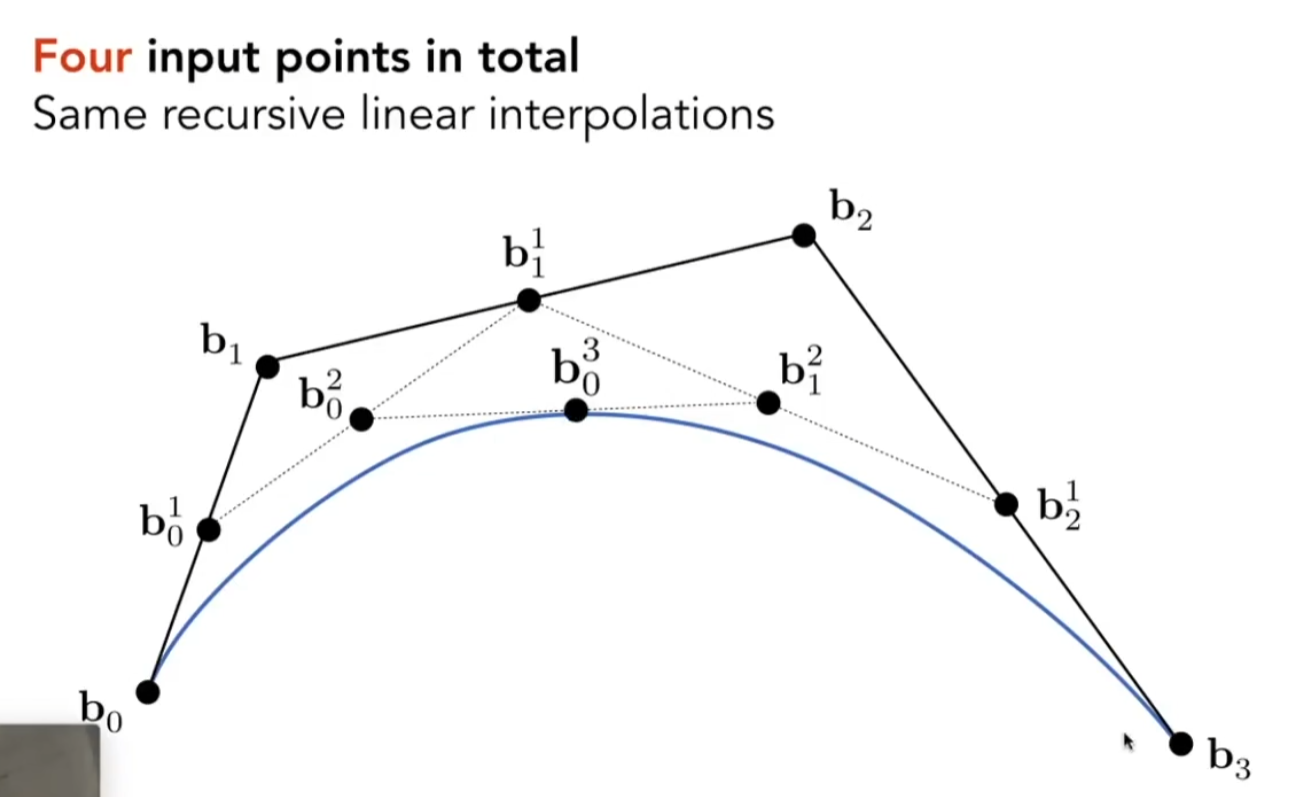
控制点的移动会造成贝塞尔曲线的移动

在每两个点间找时间t,相当于在两个点之间做线性插值

贝塞尔曲线的性质

1. 贝塞尔曲线一定过起点和终点
2. 对一个贝塞尔曲线做仿射变换,得到的新曲线和对它的控制点做仿射变换后重新画出的曲线相同
3. 贝塞尔曲线一定在几个控制点组成的凸包内

逐段定义

通过过多的控制点定义一个复杂的曲线会很困难

我们可以通过定义许多简单的贝塞尔曲线,来定义一个较复杂的曲线

那么我们怎么保证连起来的曲线是光滑的呢

曲面

我们可以把曲线的定义发散到三维

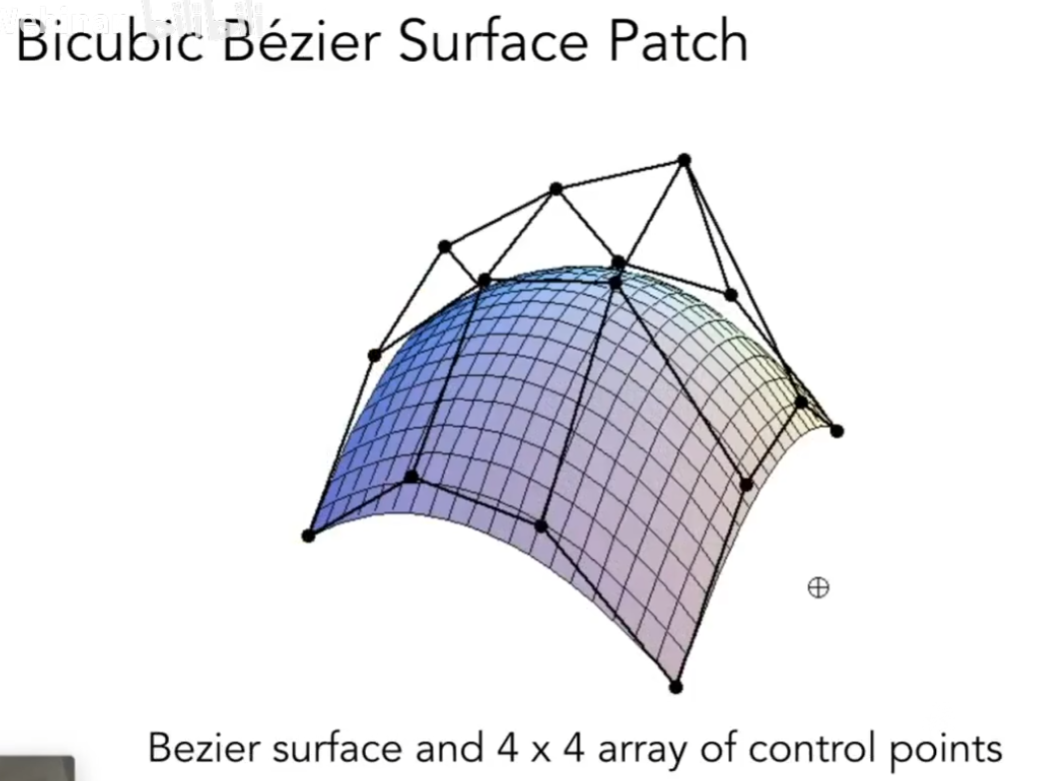
几何处理

• Mesh subdivision
• Mesh simplification
• Mesh regularization

Lecture 12:Geometry 3

Mesh Subdivision

网格细化:增加描述几何的三角形的数量

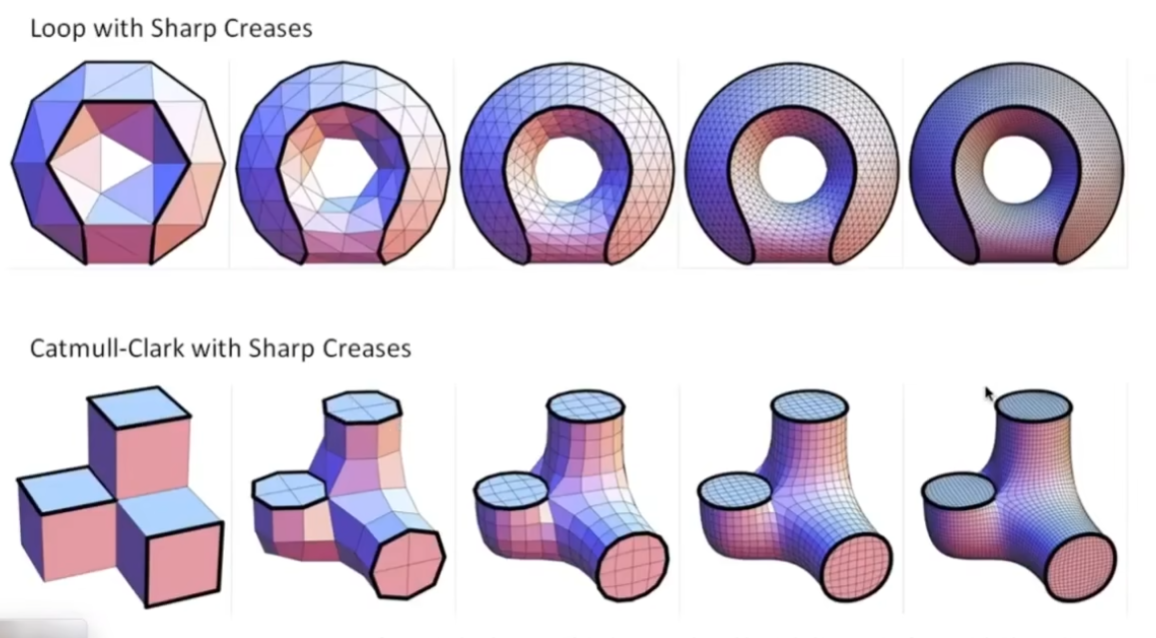
Loop Subdivision

跟循环没有关系,这个名字和海参炒面一个道理

第一步,将三角形拆分,使三角形数量增多


第二部,调整细分三角形的位置

通过某种更新方式更新定点的位置

Catmull-Clark Subdivision

定义概念

非四边形面

奇异点:度不为4的点

也就是说,只要是非四边形面的定点,就是奇异点

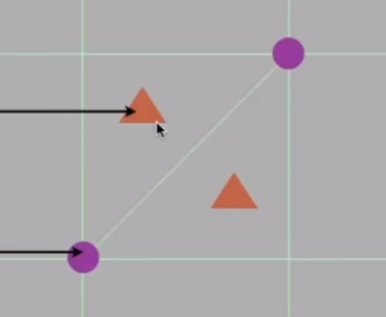
在边上取中点,在面上也取中点,将边的中点和面的中点连起来

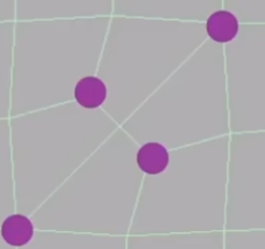
这是一次细分,经过了一次细分之后,奇异点会增加,非四边形面都消失了

那么我们可以认为每一个非四边形面引入了一个奇异点

如果我们继续做细分,奇异点数量就不会增加了

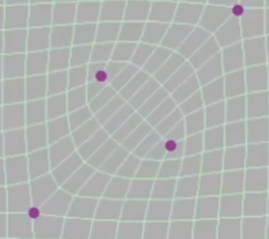
但几何将会越来越平滑

Mesh Simplification

网格简化

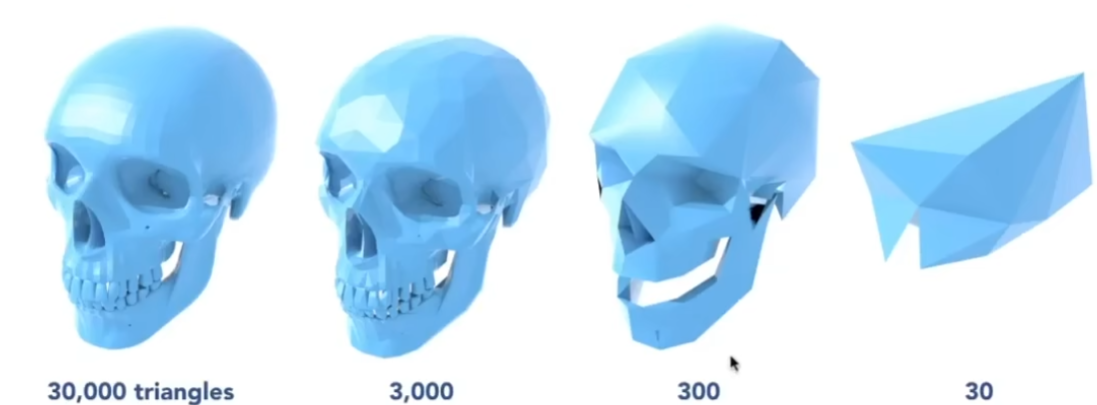
有时我们不需要太多三角形的几何,为了节省机能,我们需要将几何简化,但又不能过于简化

边坍缩

找到一个边,将这个边的两个定点合并,就可以减少面数

那么我们怎么判断坍缩哪些边呢

二次误差度量

探索后形成的点,到其原本组成的边的距离的平方叫二次度量误差

我们很容易想到,可以计算每一个边的二次度量误差,优先坍缩二次度量误差较小的点

问题在于,当坍缩一个边之后,与其相关联的边的二次度量误差会变化

使用优先队列堆结构,当进行坍塌之后,更新边的误差值

Mesh Regularization

网格正规化

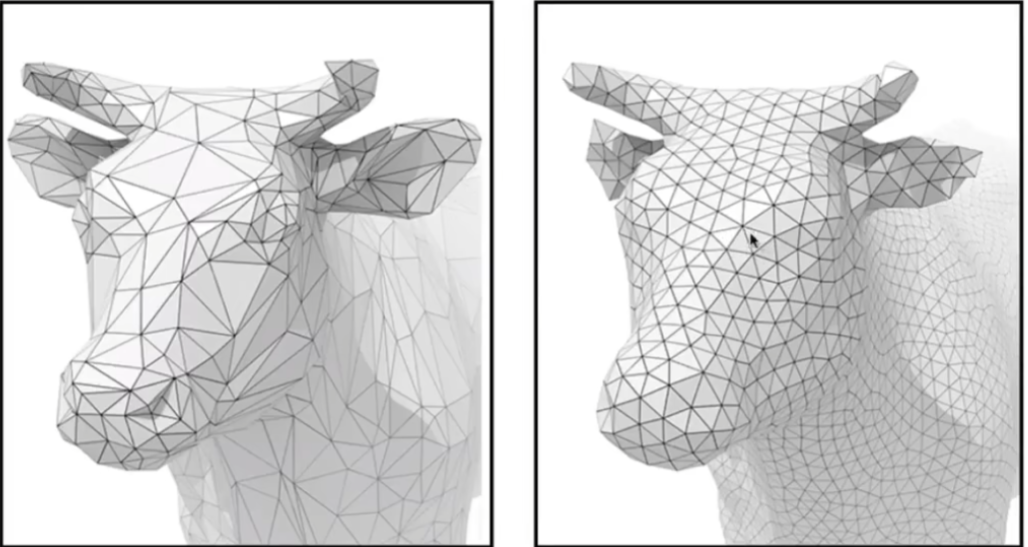
阴影

现在我们进行一个大的话题转变,我们说光线追踪

Shadow Mapping

如果我们看到一个点不在阴影里,我们又能看到这个点,说明我们可以通过摄像机看到这个点,并且光也能看到这个点

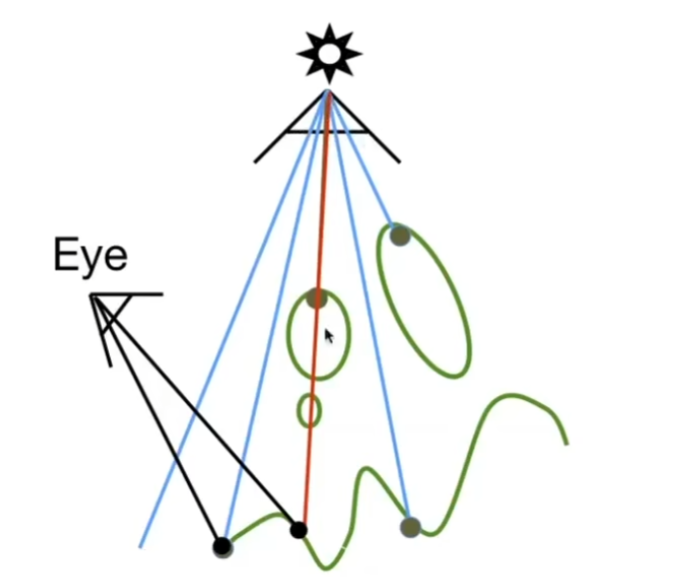
进行光源对到shadowmap的深度缓存,当摄像机看见shadowmap上不同的像素时,分析这个像素的深度和其投影到光源上的像素记录的深度是否一致

Shadow Map会出现浮点精度的问题

硬阴影和软阴影

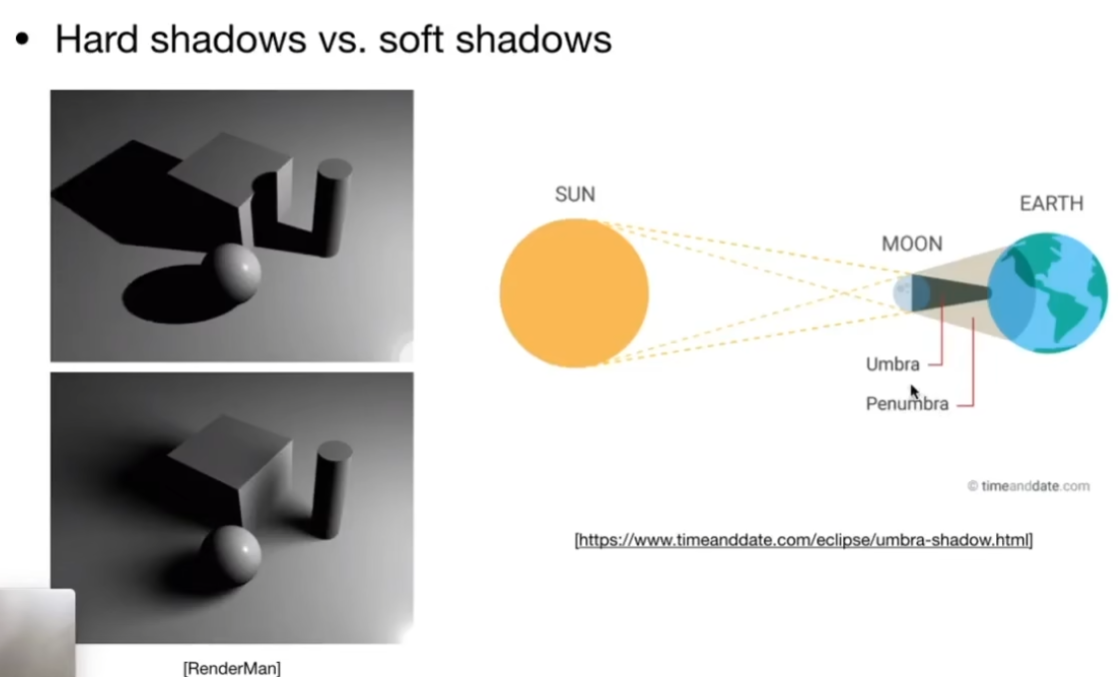
Lecture 13 Ray Tracing 1

光栅化最大的问题是无法很好的表示全局的效果,比如软阴影,Glossy reflection,间接光照

光线

1. 光线是沿着直线传播的(虽然这是错的)
2. 光线和光线不会发生碰撞(虽然依然是错的)
3. 光线从光源出发最终到达我们的眼睛

在某种语境下,我们可以认为光线可逆,也就是说眼睛可以投射”感知的射线”,如果感知的射线投射到物体上,我们就看到了物体,这就是光线追踪

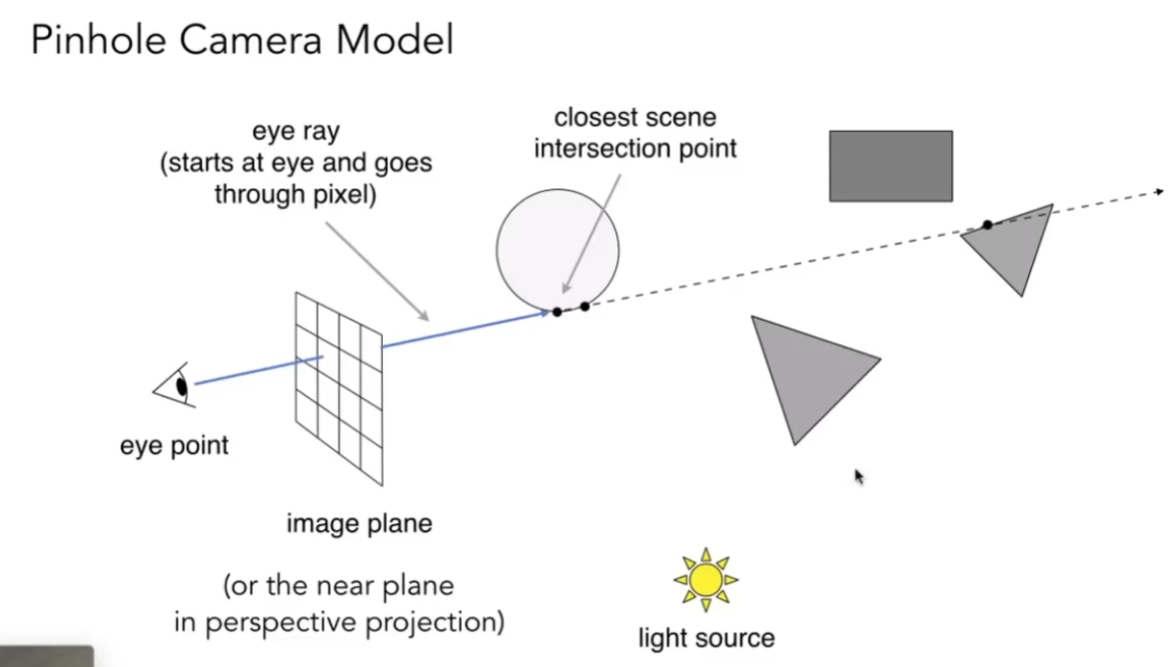
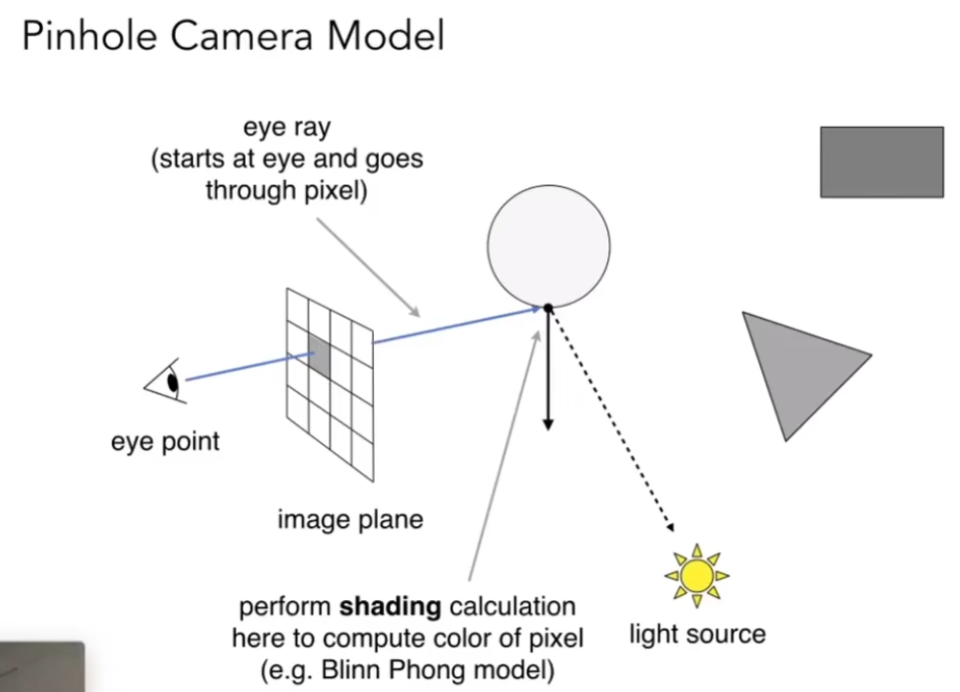
Whitted-Style Ray Tracing

当光线投射到类似玻璃的表面上,一部分能量对反射,一部分能量会折射

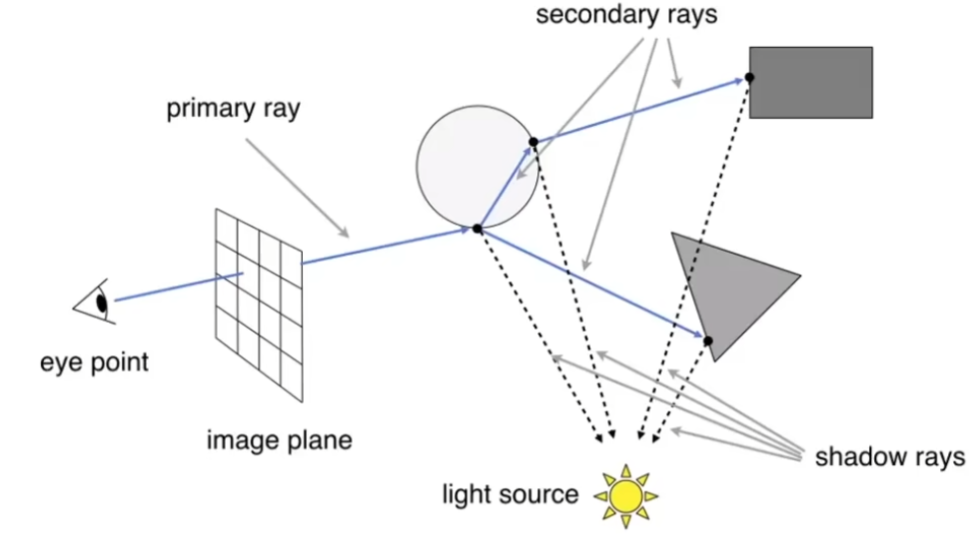
在图中,第一个打中玻璃球的点会继续向后打中3个点

我们可以在第一个打中玻璃球的点做所有点着色的加权平均

光线和物体表面的交点

交点P要满足以上两个式子

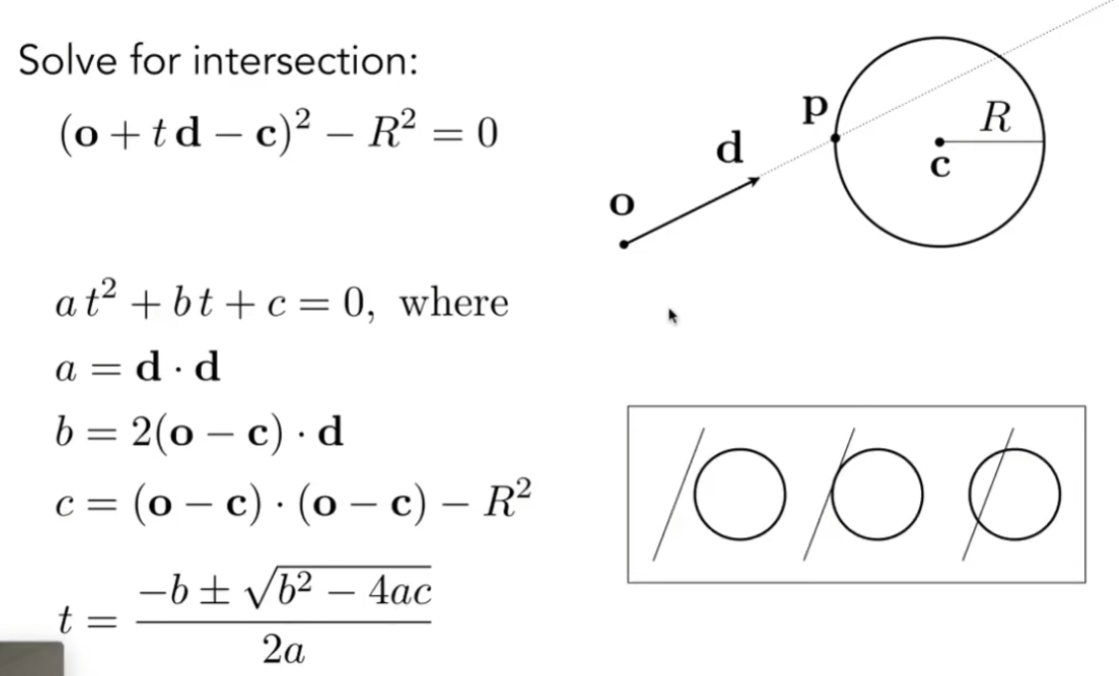
怎么样做光线和三角形的交点:

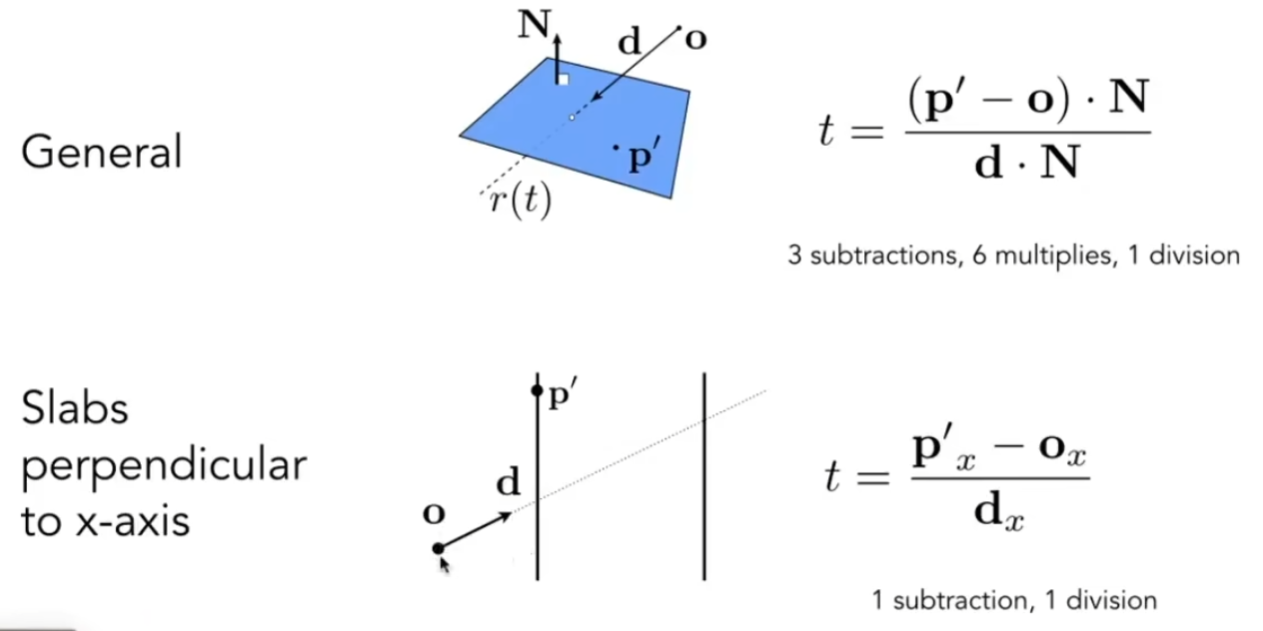
我们可以用光线和平面求交点,然后求交点是否在三角形内

点是否在三角形内的问题已经解决了,现在研究怎么让光线和平面求交

已知,交点一定又在平面上,一定又在光线上,可得计算方法

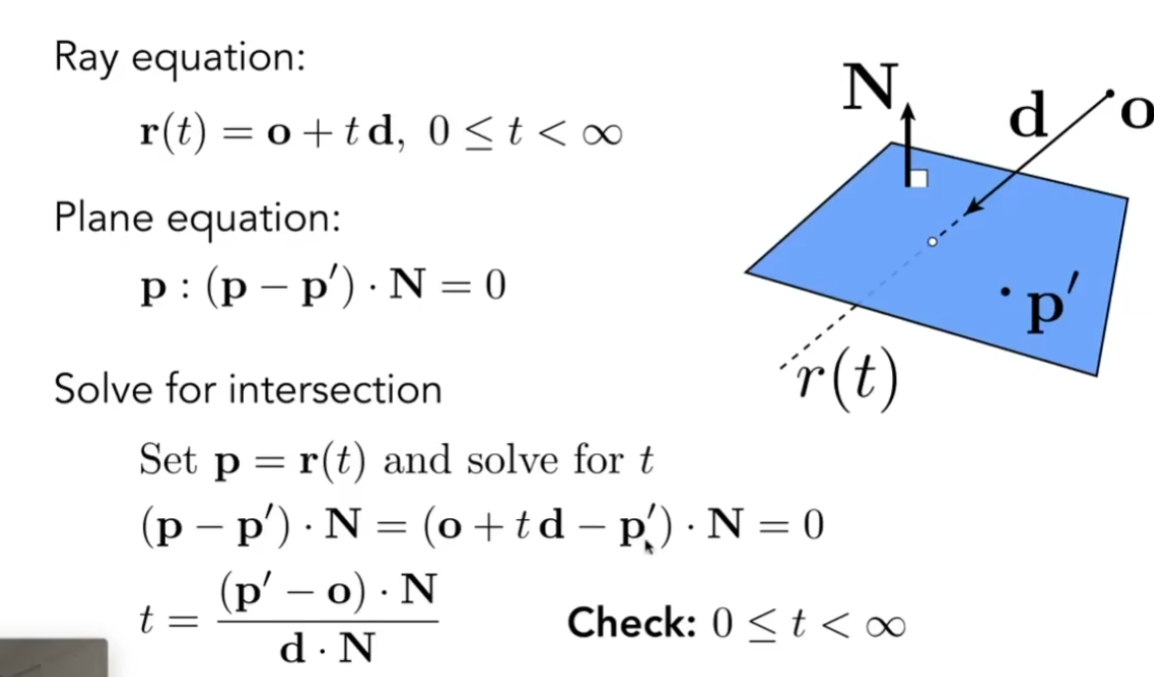
当一个场景过于复杂,我们就要计算光线与所有三角形是否有焦点,这是非常浪费机能的

包围盒(Bounding Volumes)

可以用一个简单的形状包围住一个复杂的物体

我们就可以获得一个思路,如果一个光线连物体的包围盒都碰不到,说明这个光线也不可能碰到这个物体

长方体包围盒

我们可以用3个对面定义一个长方体

怎么判断一个光线和包围盒有交点

只有当光线进入了所有的3个对面,光线才算进入了盒子,当光线离开了任意一个对面,光线就离开了盒子

对于所有光线进入对面的时间,取最大值,就是光线进入盒子的时间

离开时间同理,但取最小值

如果光线的进入时间小于离开时间,说明光线势必在盒子里待了一段时间,也说明光线一定进入了盒子

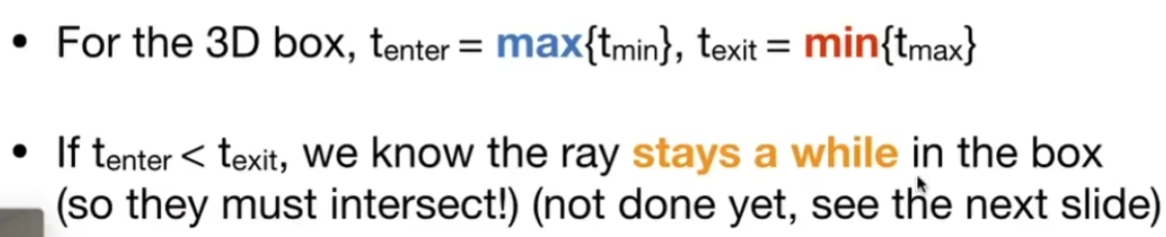
考虑负值的情况

如果一个光线的离开时间为负,说明盒子在光线后面,不可能有焦点

如果一个光线的离开时间不为负,且进入时间为负,说明光线起点在盒子里面,一定有交点

• 尽量让盒子的面与坐标面平行以利于计算
• 

Lecture 14:Ray Tracing 2

使用AABB加速光线追踪

创建包围盒,使用光线追踪之前,我们可以把包围盒分成许多小格子,标记可能有物体的小格子

如果小格子的数量适中,我们就可以用光线和小格子求交来加速判断光线是否和物体求交

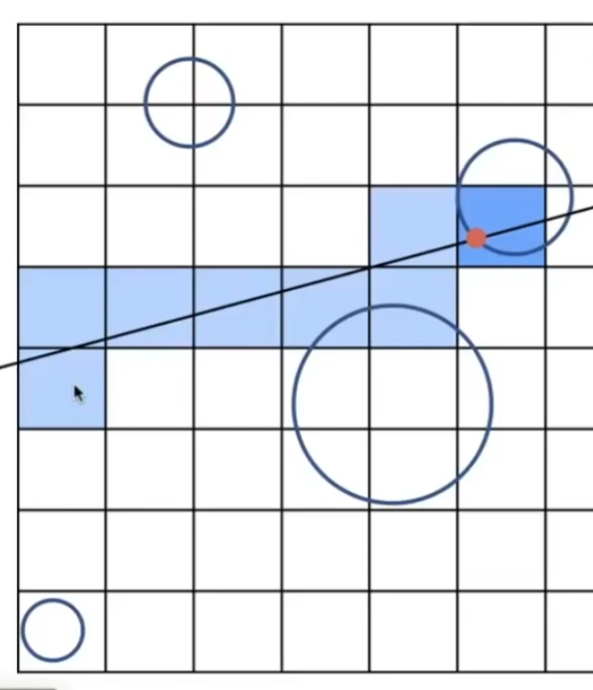
划分格子的方法

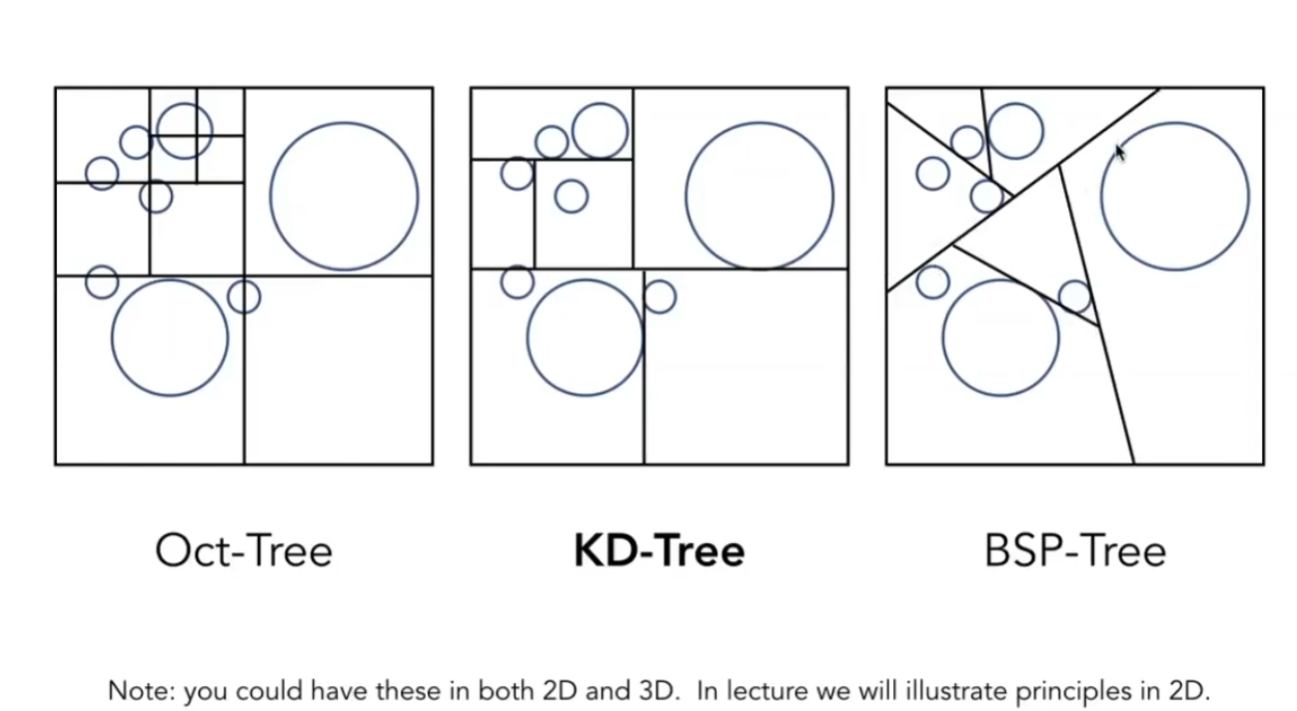
划分KDtree的过程

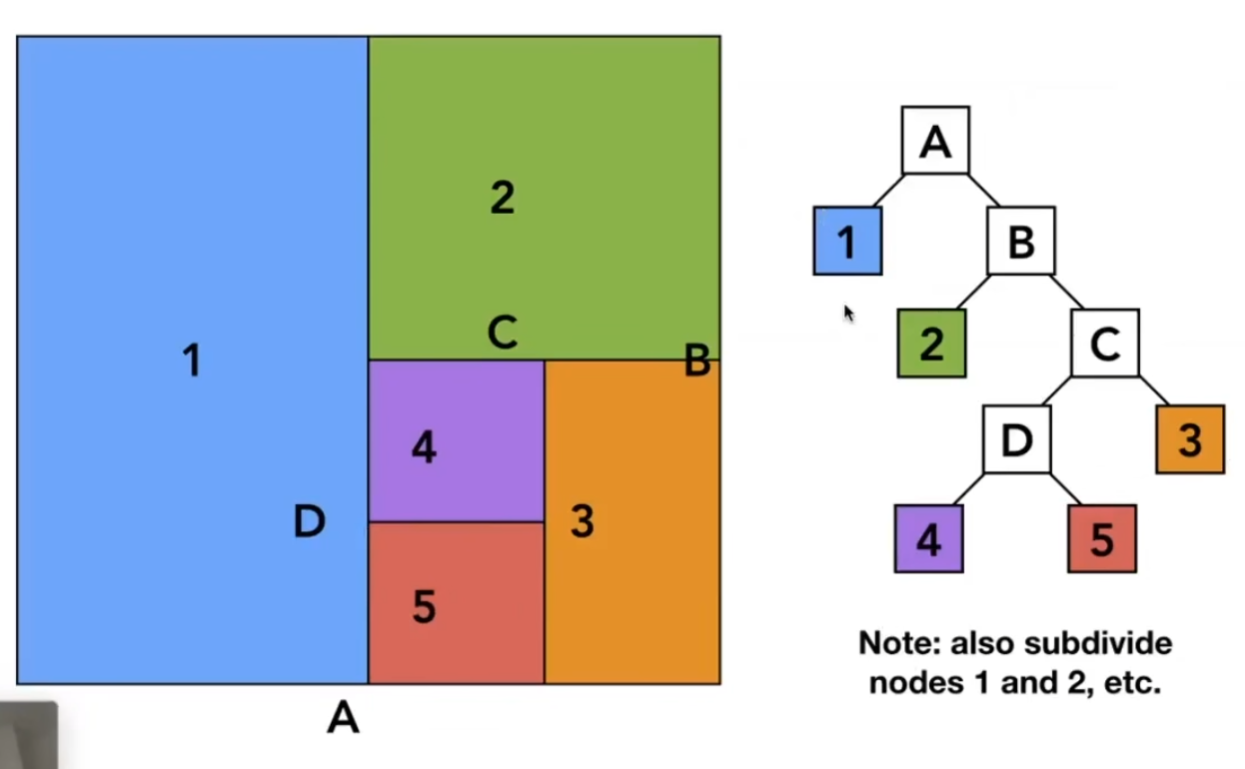
采用如此划分的加速结构,几何形体都在叶子节点上

不用一定要在中间划分

实际情况划分的细很多

如果一个光线和一个节点有交点,我们就判断这个光线是否和它的子节点有交点

如果一个光线和一个节点没有交点,我们就认为这个光线和它的所有子节点都没有交点

KDTree存在许多问题,现在已经被淘汰了

使用BVH加速光线追踪

将一个盒子中的所有三角形组织成两部分,在各个部分上继续划分成两部分

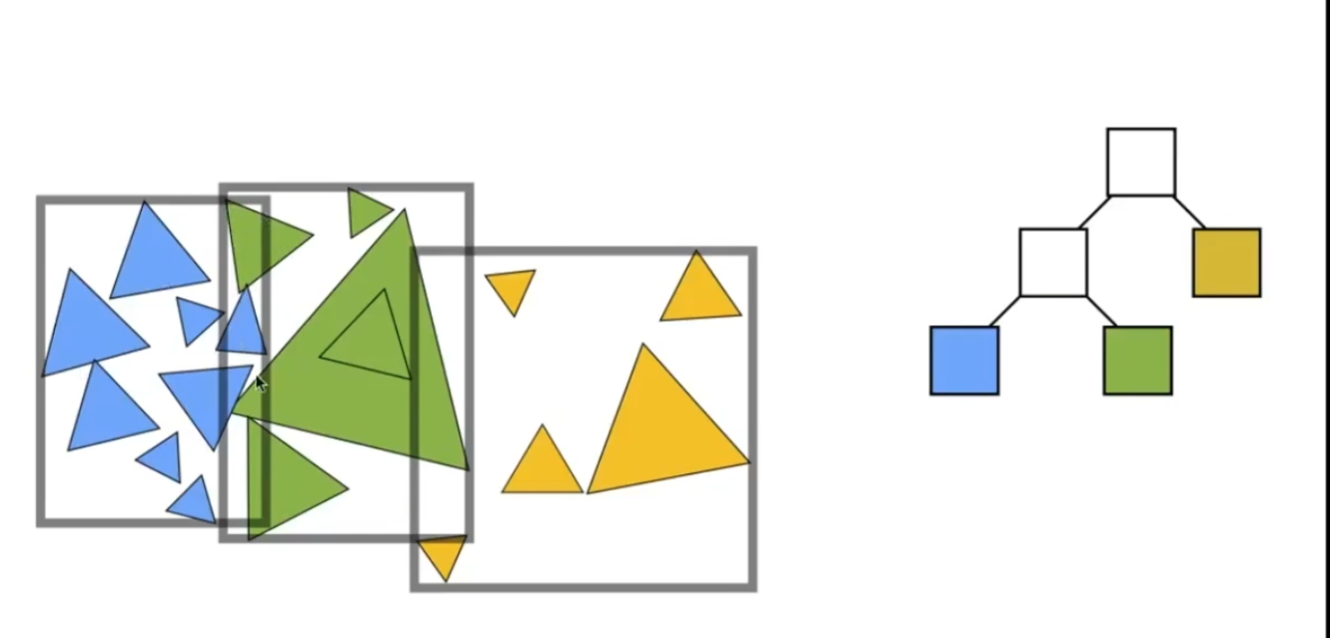
关于如何划分:

取中间的三角形,也就是位置是中位数的三角形来划分,目的是让树的两端更平衡

取三角形的重心判断三角形的位置

关于算法:

给你n个数,找它们的中位数,也就是第1/2*n大的数,可以用快速选择算法

关于逻辑:

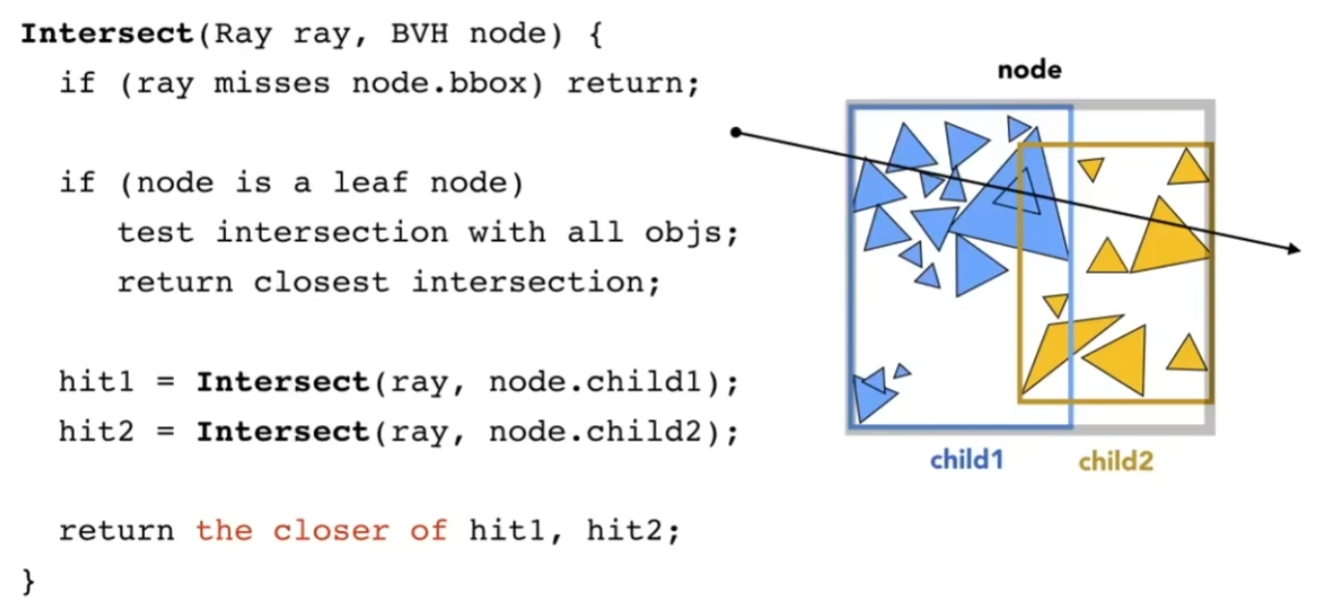
辐射度量学(basic radiometry)

下面介绍一些必要的物理量

Radiant Energy

Q[J=Joule]

Radiant flux(power)

表示单位时间内的能量


光源会辐射各种不同的能量,物体表面也会接收不同的能量,光在传播的过程中能量也会发生变化,我们分别介绍物理量

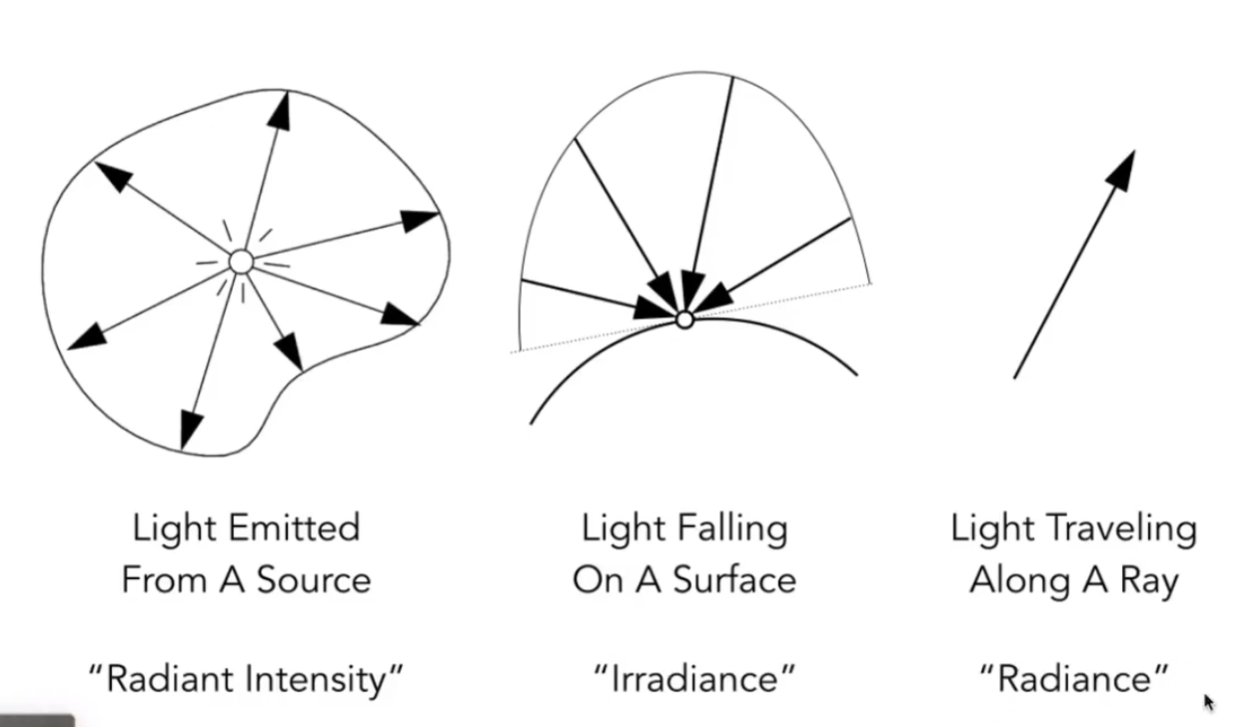
Radiant Intensity

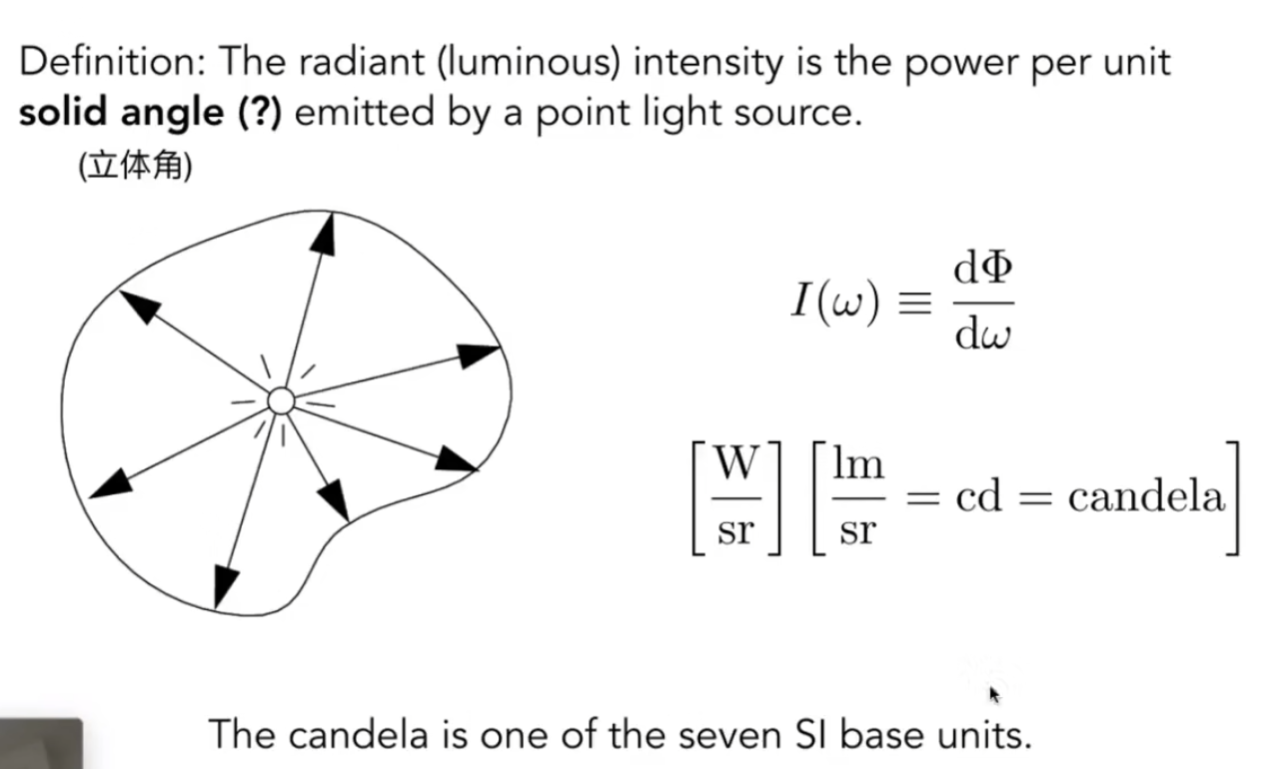
立体角

如何定义一个角?弧长除以半径是个好办法

而立体角是弧度制在三围的延伸

定义立体角:面积除以半径的平方

微分立体角

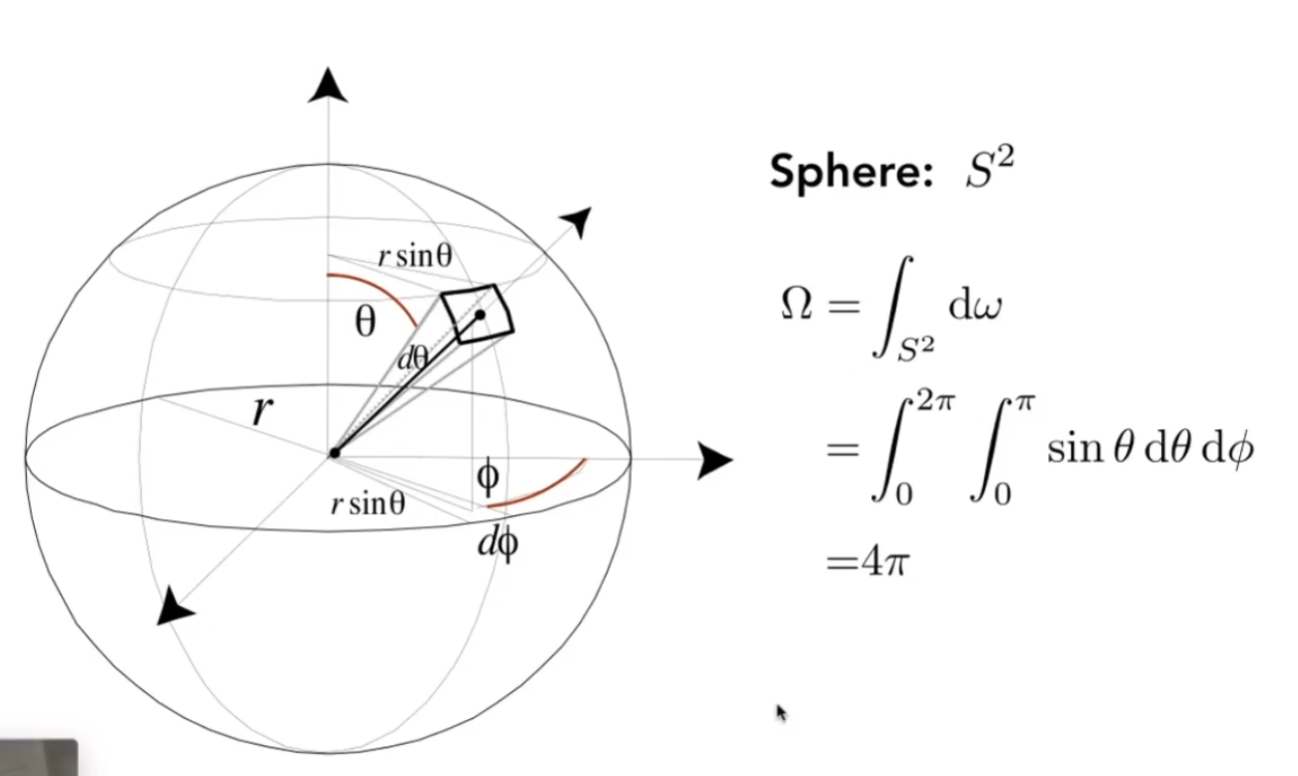
现在说回Radiant Intensity,如果一个点在所有方向辐射的能量是均匀的,Radiant Intensity表示一个点光源在各个方向上的能量

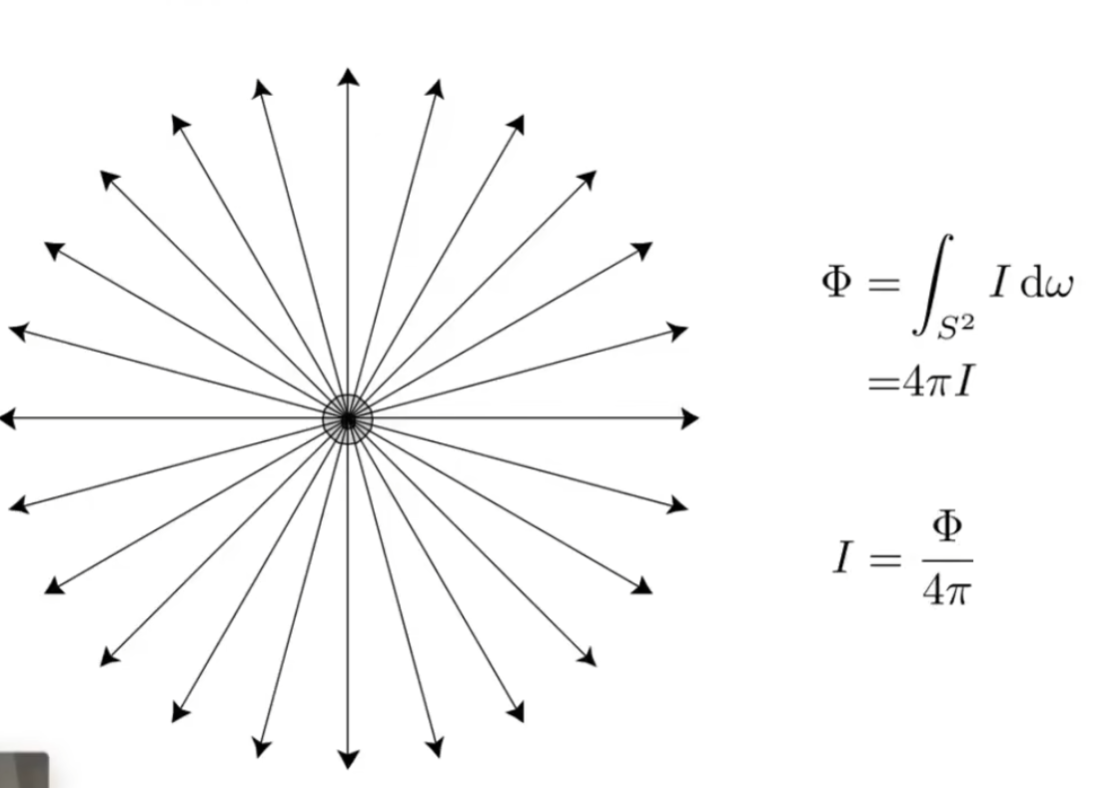
Ray Tracing3

继续介绍物理量

Irradiance

每面积上对应的功率

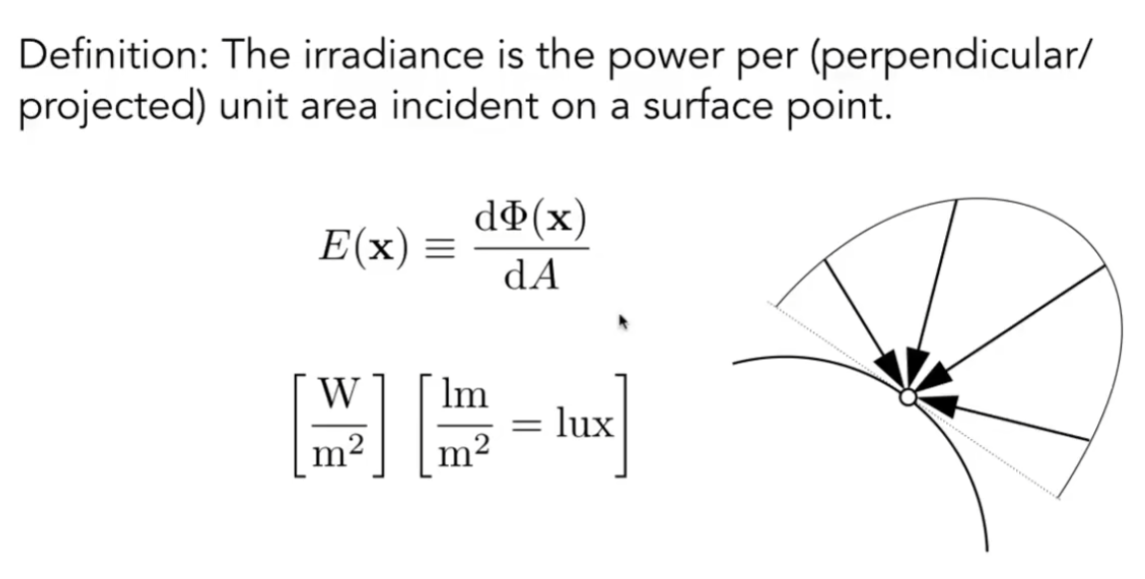
投影到垂直光线方向的面积,才是合法的面积

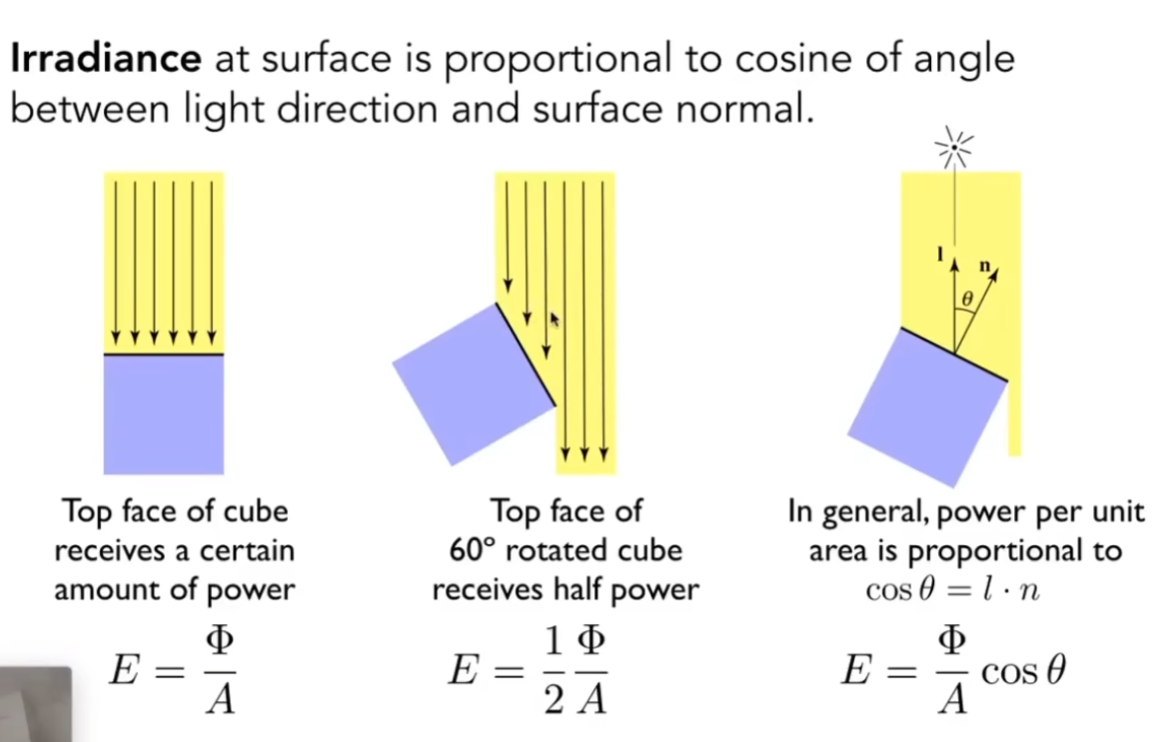
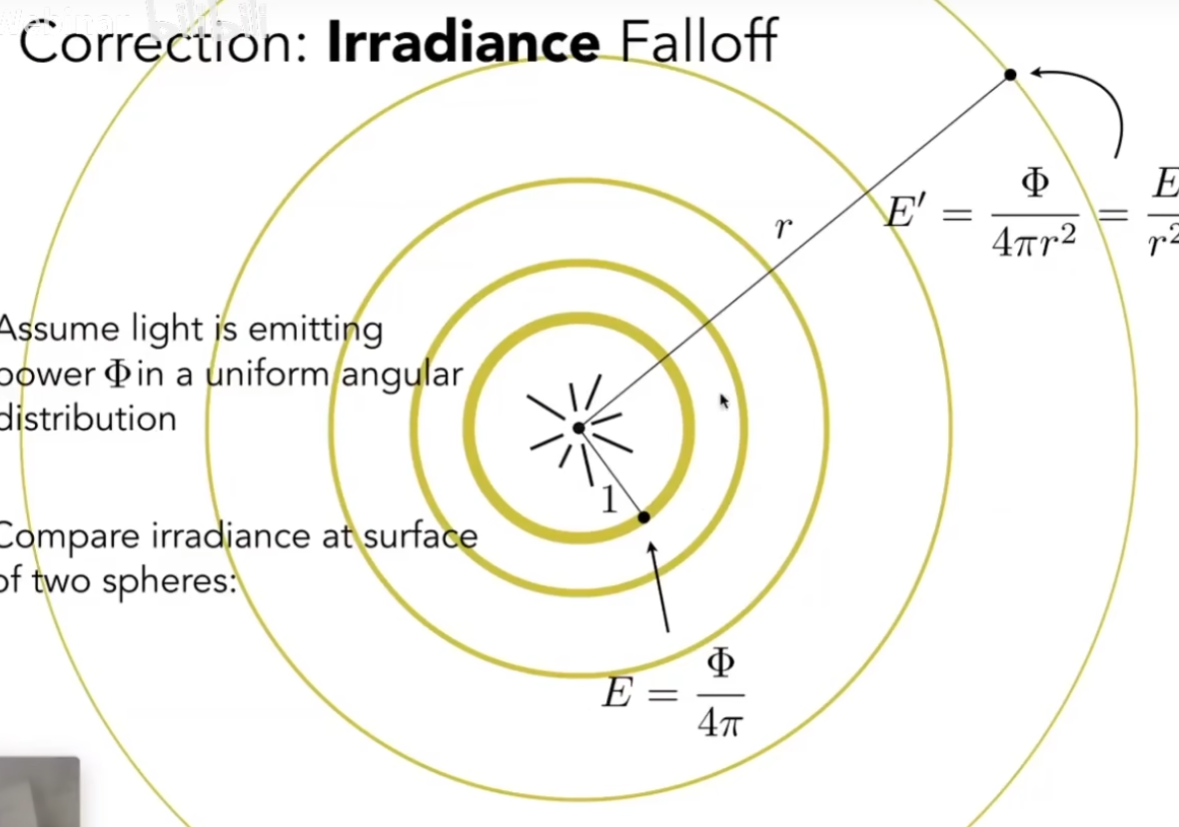
当点光源的能量随传播衰减时,是Irradiance在衰减,而不是Intensity在衰减

Radiance

每面积*立体角上的功率

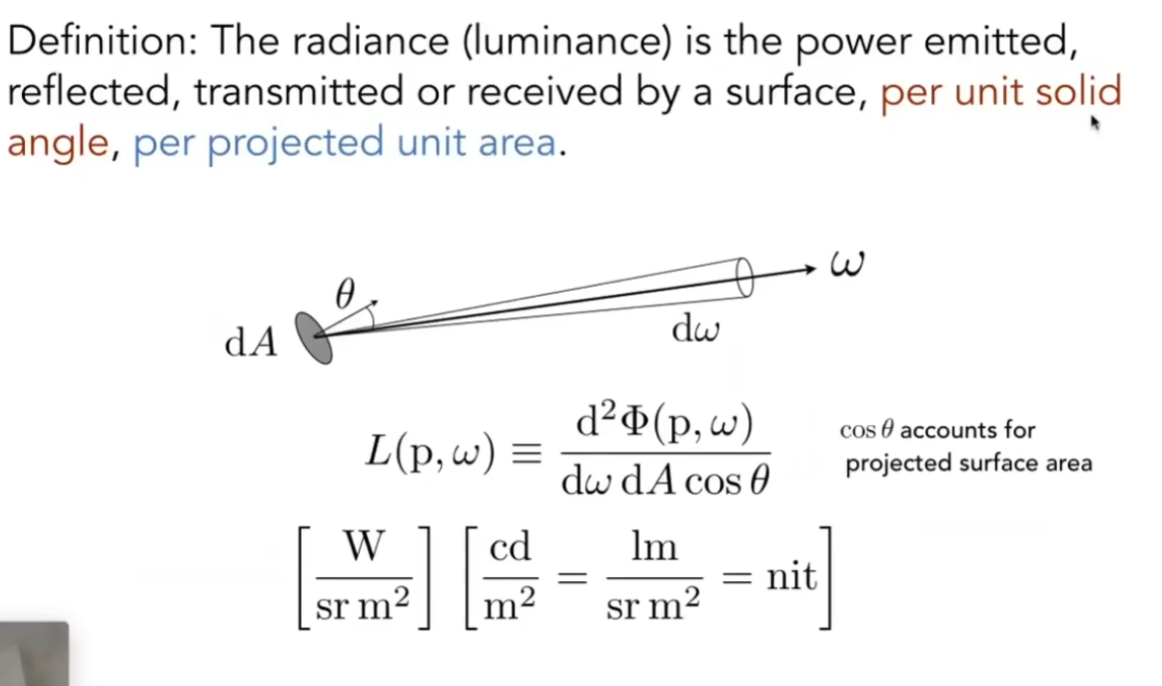
所以,Radiance也可以理解为每立体角Irradiance,也可以理解为每面积Intensity

Irradiance和Radiance的关系

Irradiance表示每面积收到的能量,Radiance表示面积在某一个方向上收到的能量

所以Irradiance也表示每面积将所有方向的能量积分起来

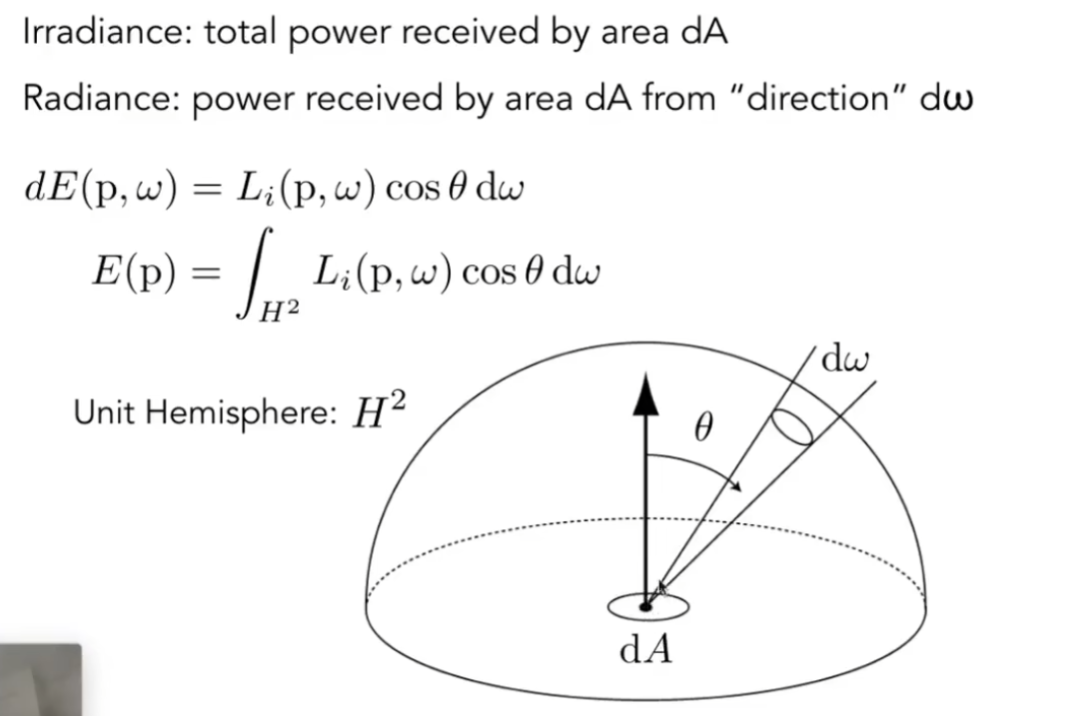
BRDF(双向反射分布函数)

当光打中了一个物体,会反射, 我们可以如此理解

光改变了一个方向

也可以换一种方式理解

光的能量被吸收了,然后物体又在另一个方向将能量释放了出去

一个小面积如何将光反射出去,就是BRDF的定义

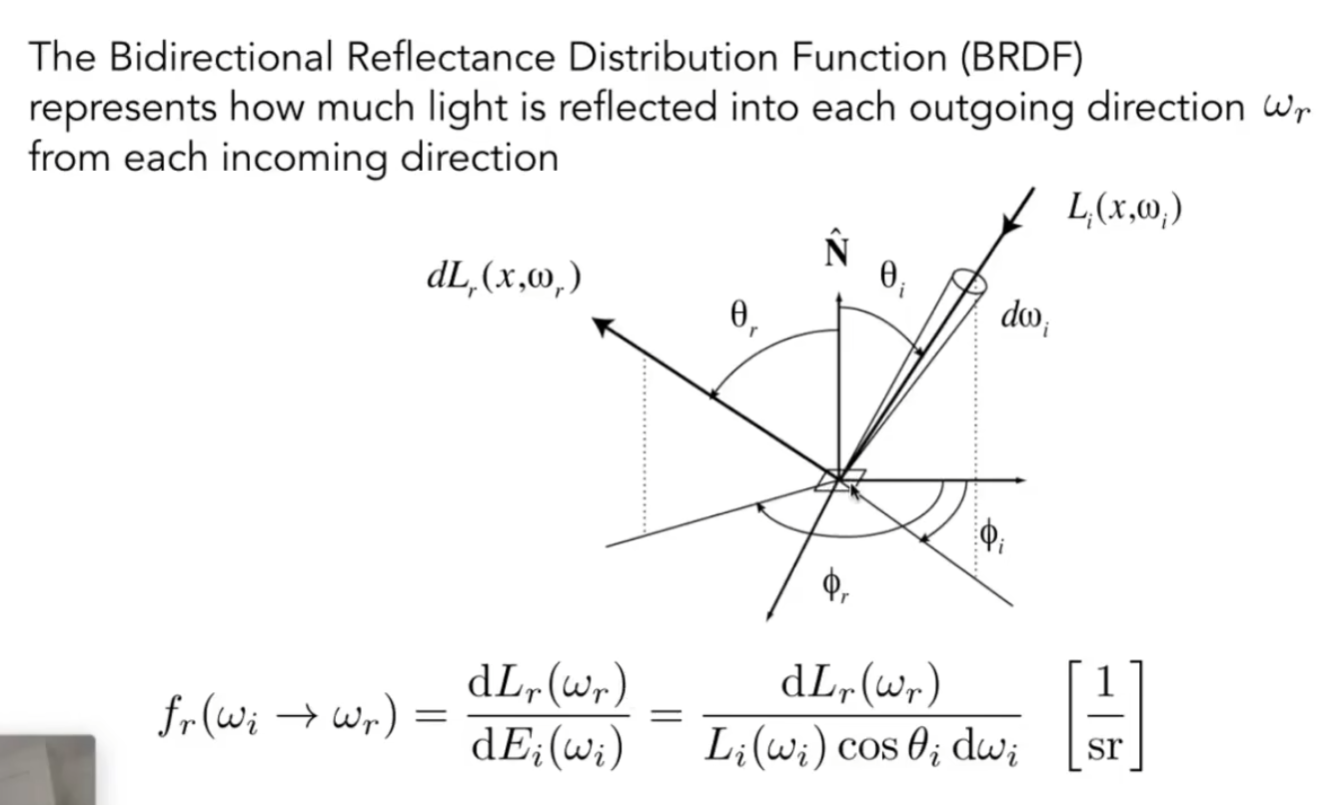
一个点可以接收各种不同方向的光,对于这个点反射的某一方向的光,可以将所有方向入射的光对这个反射方向的贡献加和,就得到了该反射方向的光

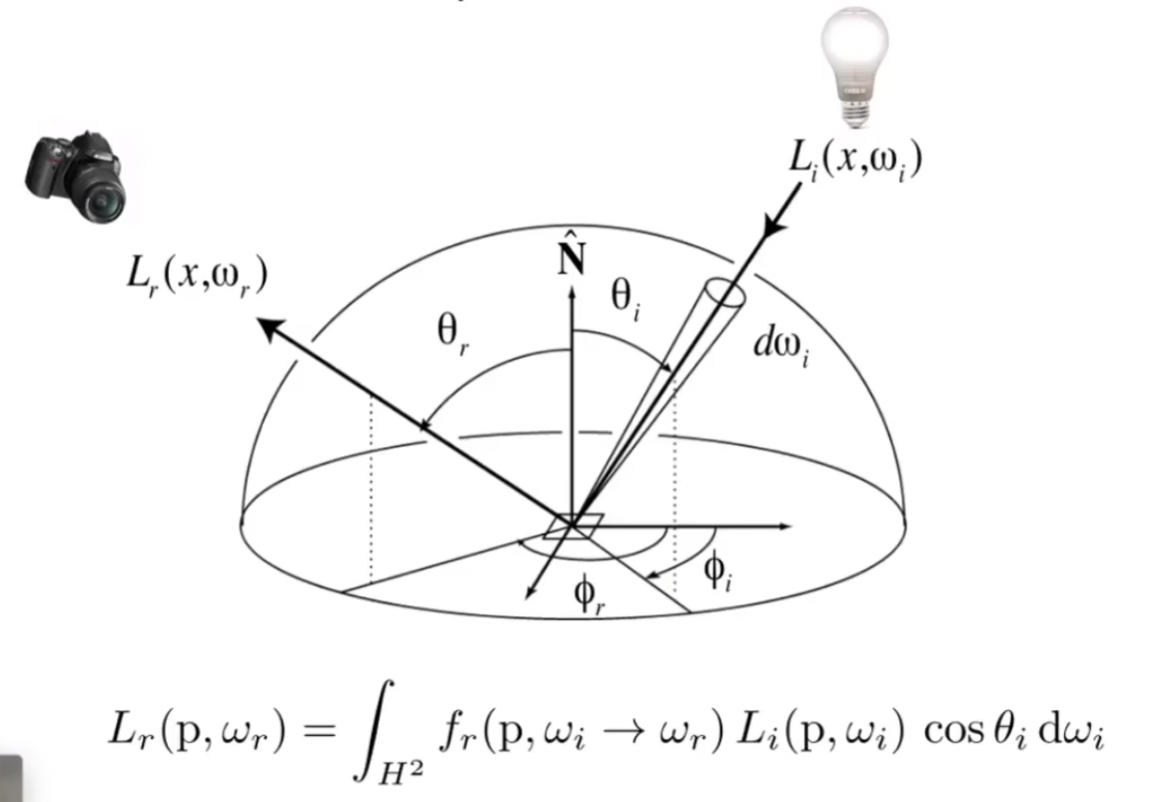
如果这个物体会发光,那这个方程该怎么算?

很简单,把发出的光加上就行

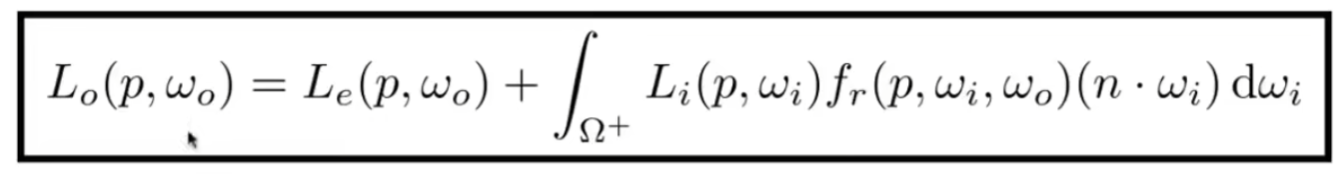
以上方程称为渲染方程

理解渲染方程

有一个面光源,我们可以我们将它理解为一个点光源的集合

在计算上我们可以将这个面光源积分


简化写法

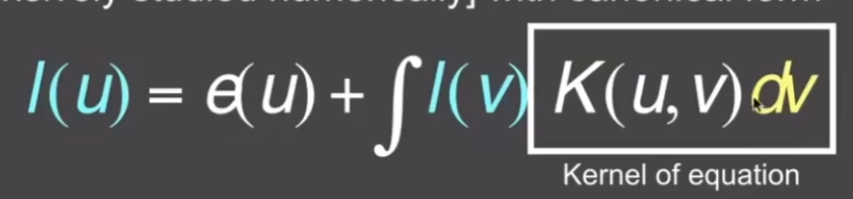
再简化写法

L指所有物体辐射的所有能量,E指所有光源辐射的能量,KL指所有能量被反射出的能量,可以将K理解为反射操作符

我们将渲染方程如此简化,是为了,解渲染方程

也就是说,L等于所有光源辐射的能量,加所有光源辐射能量弹射一次的能量,加弹射两次的能量,加……

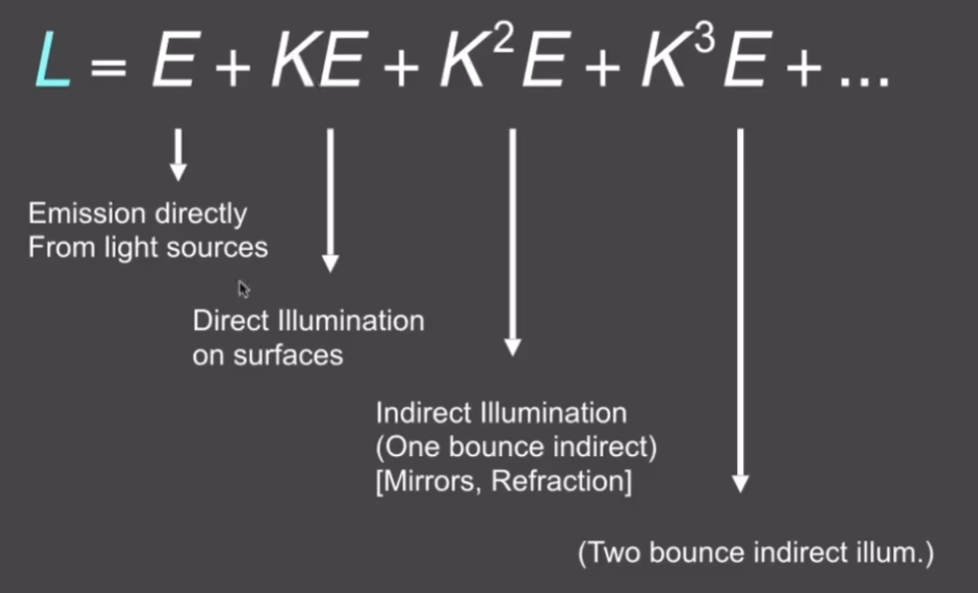
光线不弹射叫直接光照

光线弹射之后的光照叫间接光照

直接光照和间接光照的和叫全局光照

着色做的就是直接光照

光栅化能告诉我们的光照的内容就只有E+KE,后面的部分光栅化比较难做

以下是示例

只有直接光照

加上一次间接光照

加上两次间接光照

概率论回顾

是的,学图形学害得学概率论

Ray Tracing4(Monte Carlo Path Tracing)

蒙特拉罗积分

给出任意一个函数,为了算出它从a到b的定积分,我们会写出函数的解析式

但如果这个函数非常复杂,无法写出解析式,我们可以使用蒙特卡罗积分

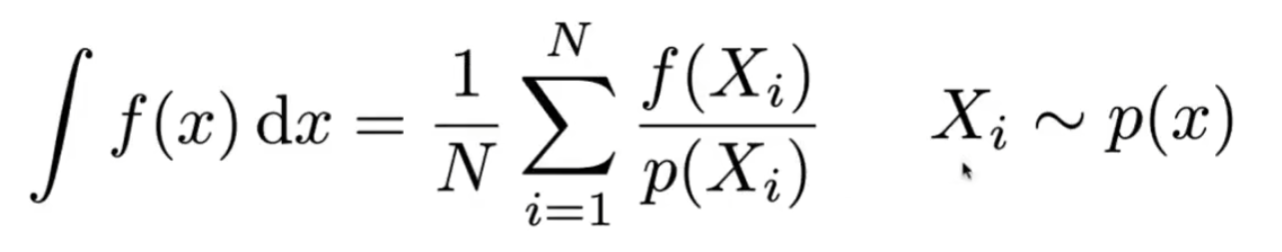
路径追踪

我们已经学过了Whitted-stylle Ray Tracing,它认为如果一个光线打中了一个透明物品,那么光线就会折射,如果光线打中了一个漫反射的物体,那么光线就会截止,这是不对的

如何解决Whitted-stylle Ray Tracing的问题

首先,我们知道Whitted-stylle Ray Tracing是错的,但我们知道渲染方程是对的


Lecture 17 Materials and Appearances

外观是光线和材质共同作用的结果

材质=BRDF

材质的种类

Glossy material

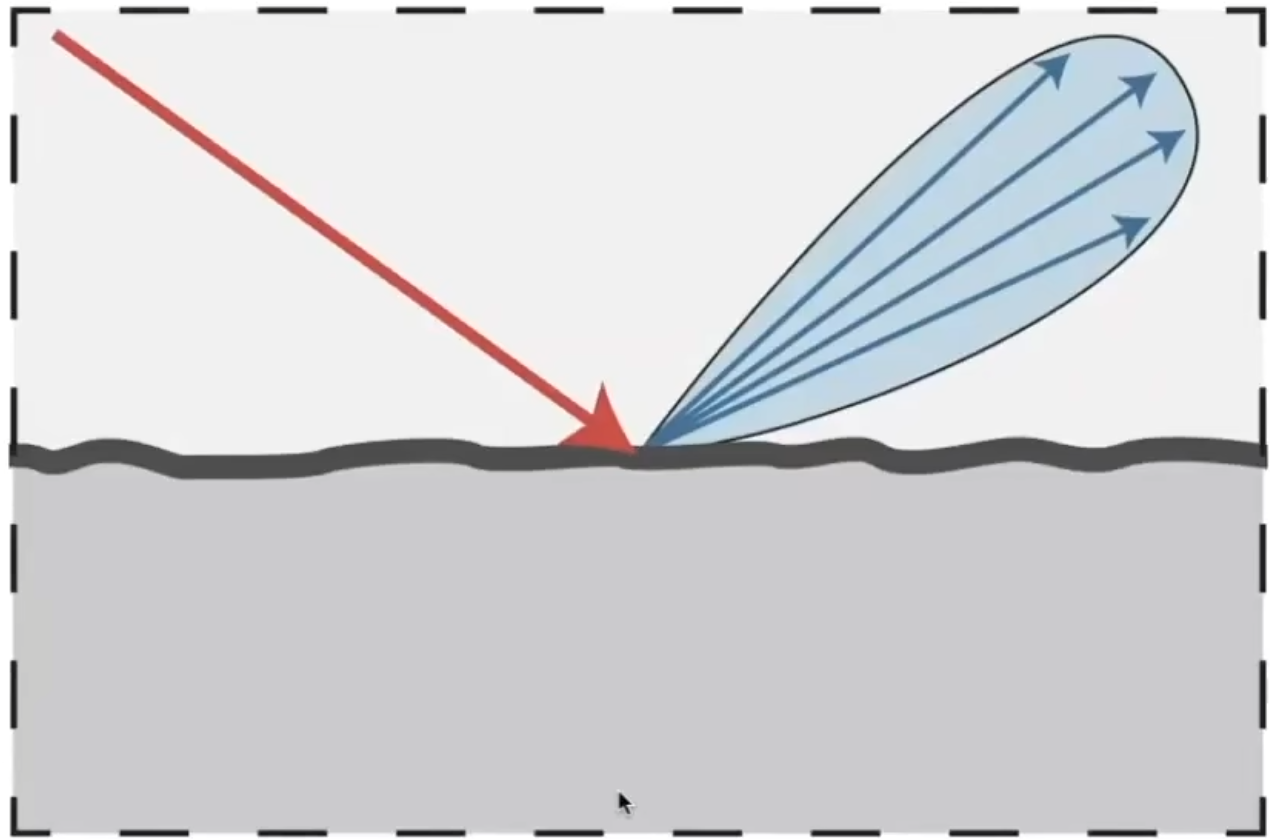
Ideal reflective/refractive material

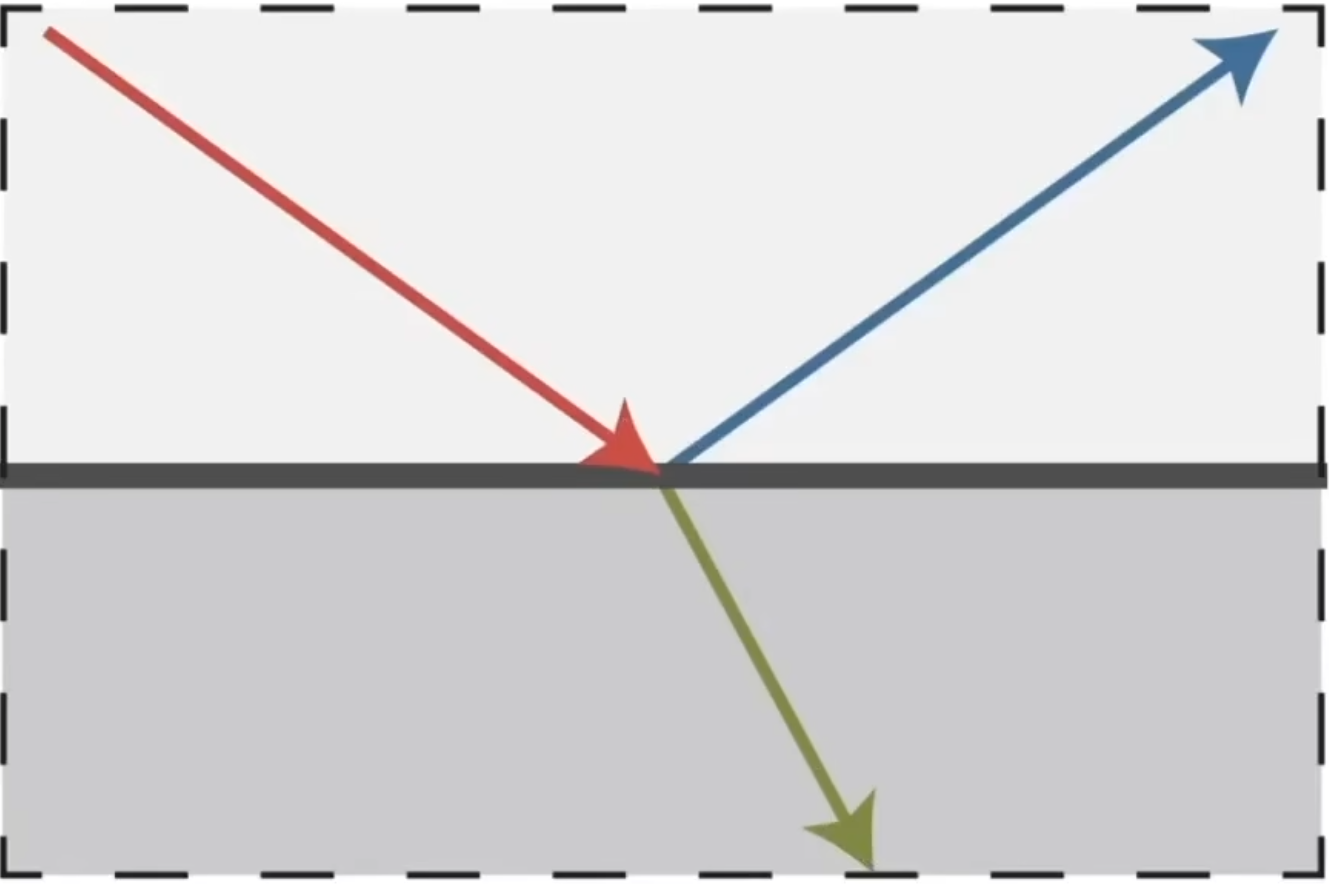
折射

如何计算折射

折射定律

如果我们定义入射光线和出射光线的角度,那么只要我们定义折射率,也就是这两个角度之间的关系


只有当上图下方的比例大于1,根号就有可能没有意义

菲涅尔项

注意桌子上书的影子,也就是书反射的光

如果光线入射的角度和物体表面完全平行,那么可以认为所有的光都被反射,如果光线入射的角度和物体表面垂直,

Lecture 18:Advanced Topics in Rendering

蒙特卡罗估计的期望如果总是我们要的真实值,就是这个方法是无偏的估计,其他情况是有偏的

如果方法是有偏的,当我们估计的样本足够多,结果会收敛到一个近似真实值的值,称为consistent

无偏光线传播方法

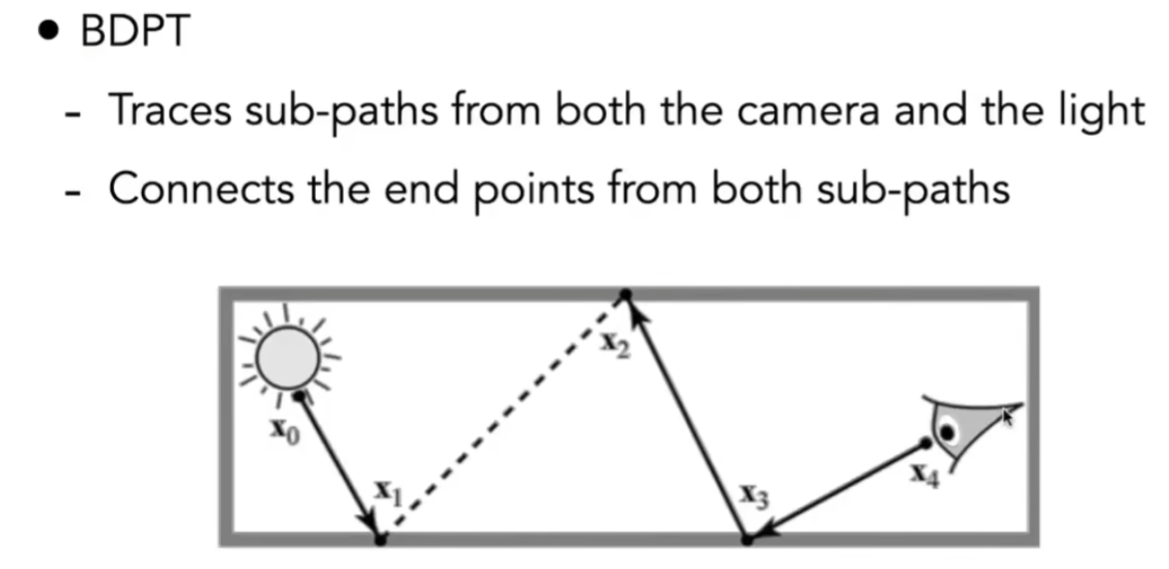
Bidirectional path tracing

生成两个不同的半路径,分别从光源和摄像机出发,最后将两个半路径的端点连接

Metropolis Light Transport

用马尔科夫链帮助采样

马尔科夫链方法是,如果你有一个样本,你可以在周围生成一个新样本

我们用这种方法, 不断在一个路径周围寻找新的路径,就可以找到所有的路径

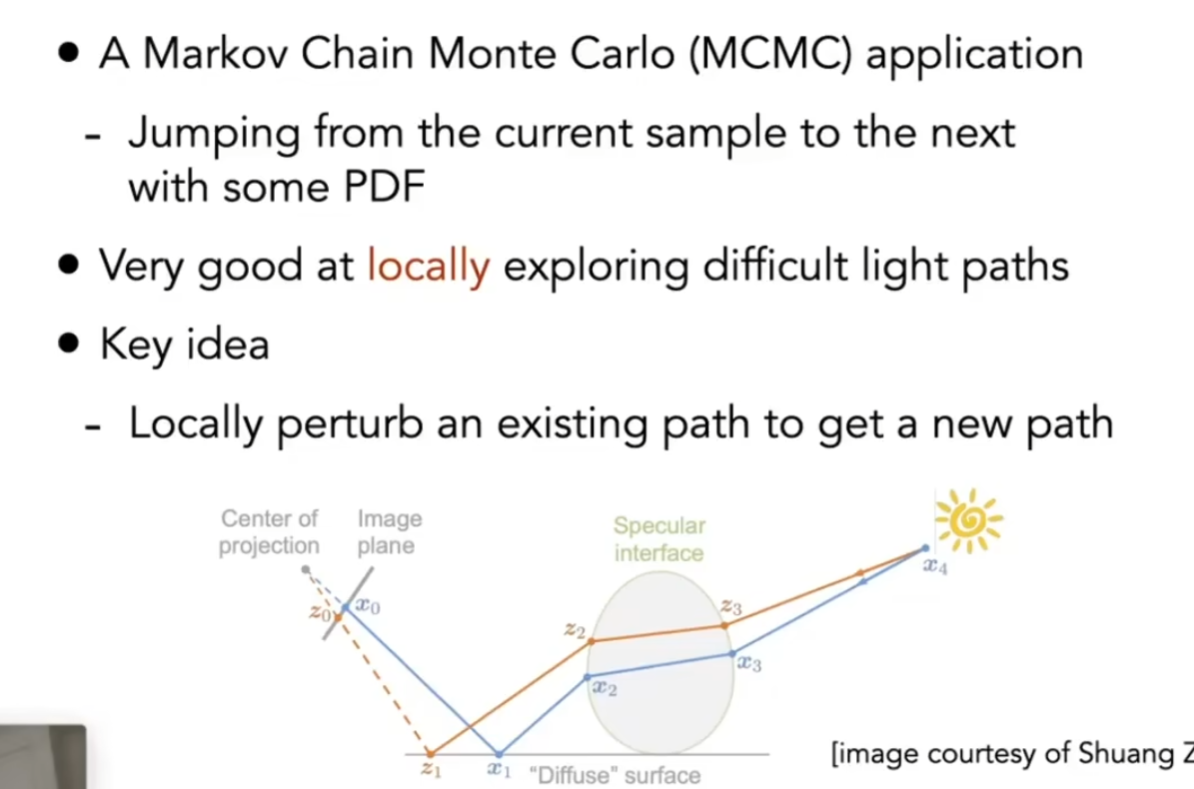
Metropolis方法很难在理论上估计收敛的速度,同时所有的操作是局部的,所以可能有的像素收敛的慢,有的像素收敛的快,会使得到的图像很脏

有偏光线传播方法

Photon Mappin光子映射

一种光子映射的实现方法

第一步,从光源出发.光源无时无刻在向外辐射光子,如果光子打中物体,可能反射也可能折射,但当光子打中diffuse surface上,光子就会停止

第二步,从摄像机开始,向外发射路径(sub-path),路径打中物体,也会反射和折射,但当路径打中diffuse surface上,路径就会停止

最后,进行local density estimation,也就是说,对于任何着色点,找到它最近的n个光子,得到所有光子所占的面的面积,然后计算光子的密度(数量/面积)

当光子的密度越高,就越接近真实

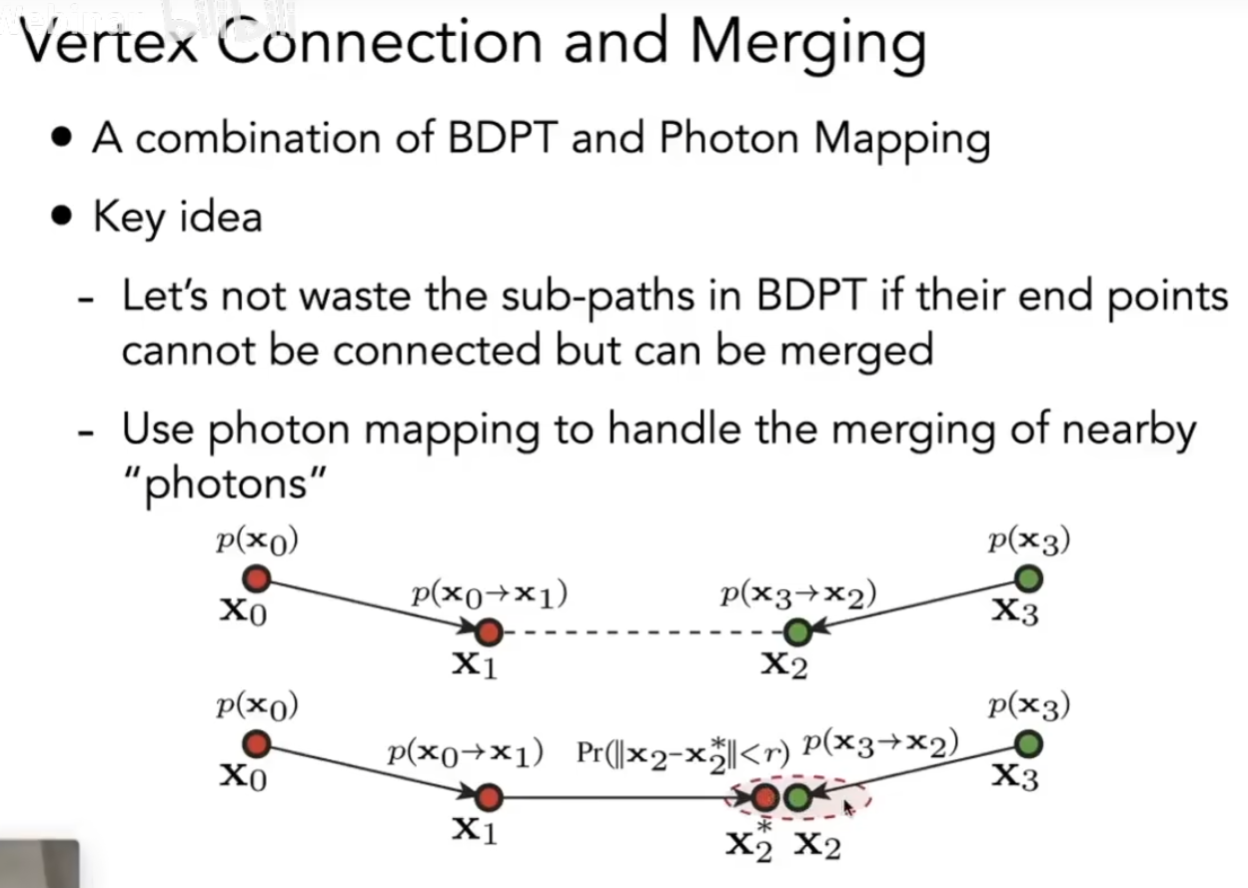
Vertex Connection and Merging

Instant Radiosity

我们可以不区分光线是光源发射出来的,还是光反射出来的,我们可以认为只要是光达到的物体,就变成了新的光源

散射介质

当光线行进的过程中,散射介质中会有晶体将光线向各个方向反射

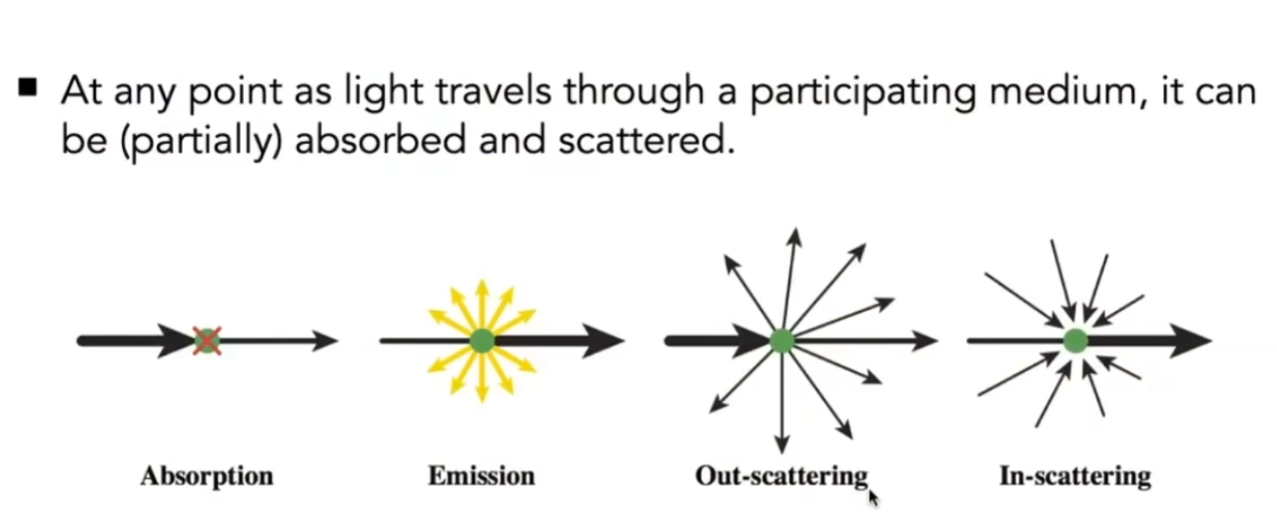
光线在传播的过程中会被吸收,被反射

这个反射,由Phase Function决定

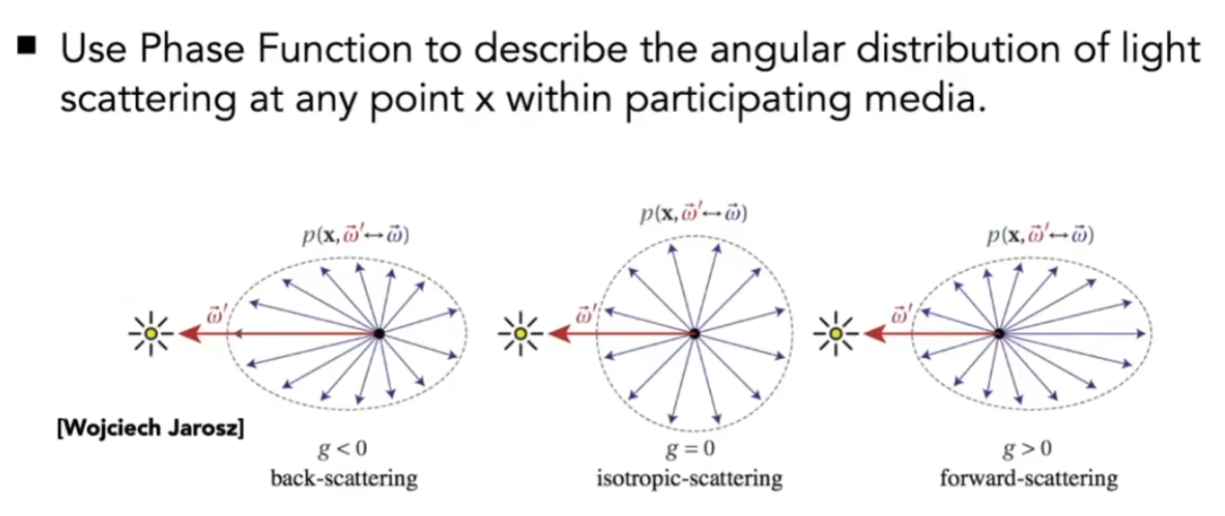
Marschner Model

当一个光线打中一个圆柱,有一部分光会被反射,另一部分会穿过去,在圆柱的内壁上再次反射穿出来

如果模拟头发,那么光线会在头发间不断的反射,最终弹射出来被摄像机看见,计算量是巨大的

这个办法可以描述人的毛发,但描述动物的毛发会有问题,动物的毛发中有更多的髓质,可以看成散射介质

Double Cylinder Model

将动物的毛发看成是两个圆柱,内部的圆柱是散射介质

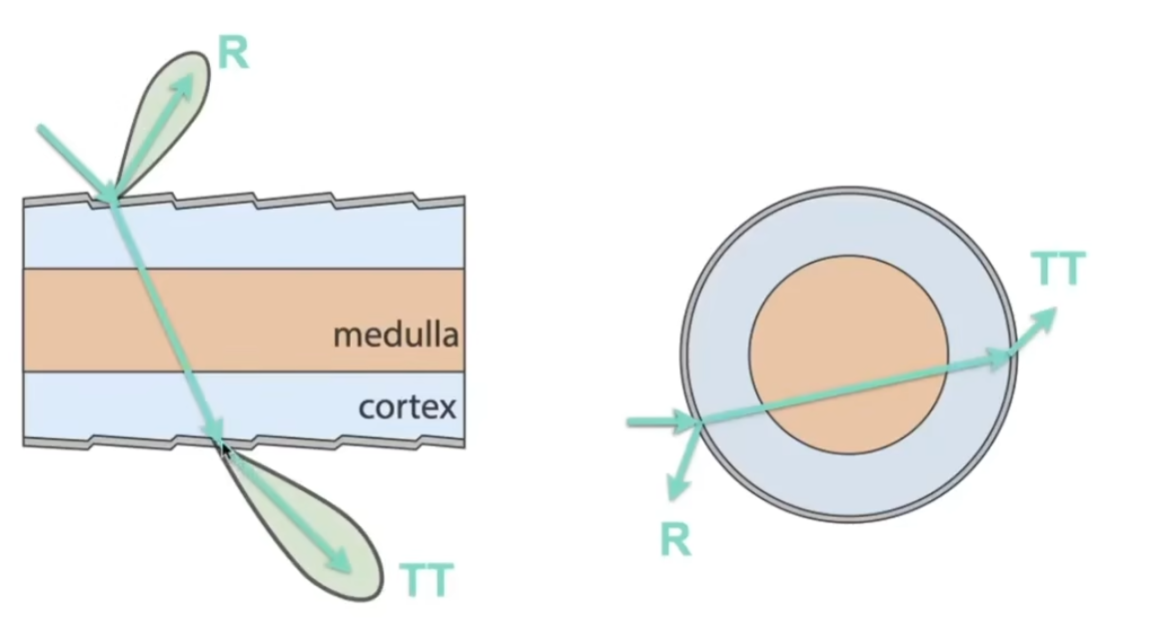
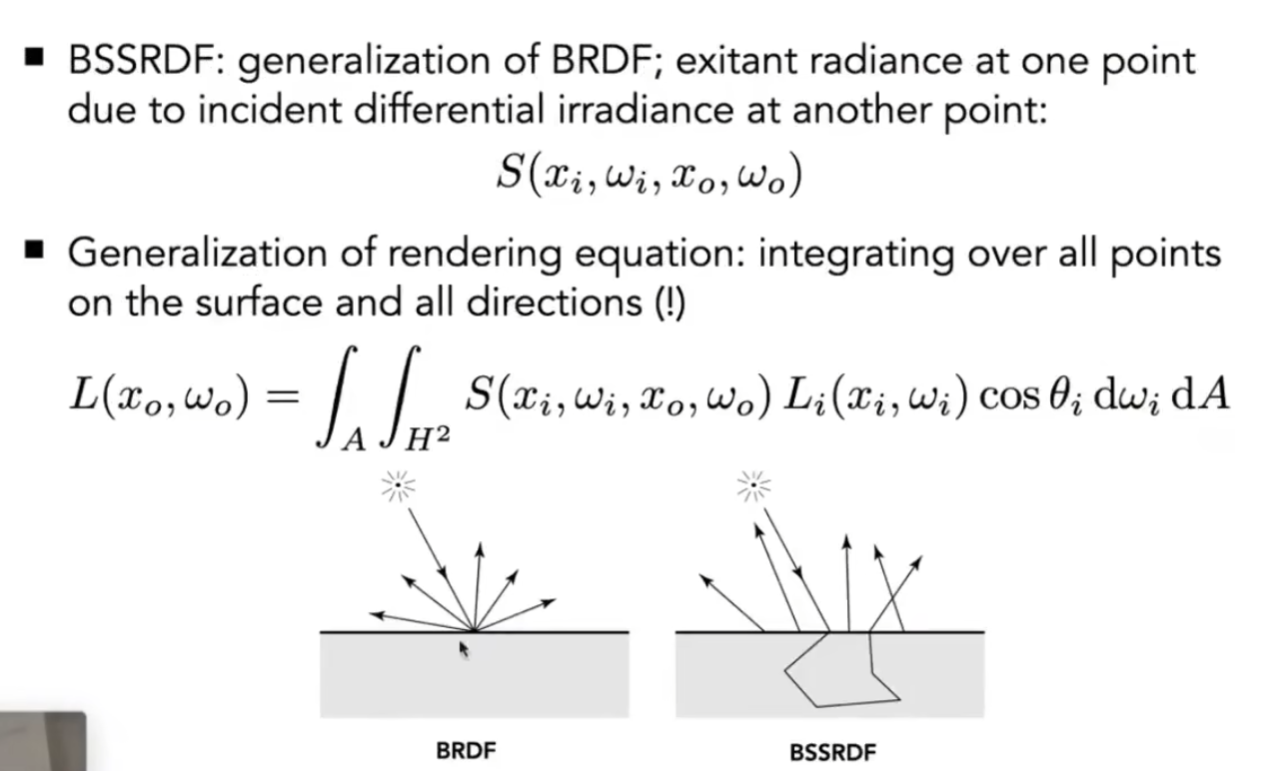
surface model

Subsurface model

Cloth

布料是一系列缠绕的纤维,纤维的缠绕有层级

所以布料的渲染和纤维的缠绕方法有关

Lecture 19:Cameras,Lenses and Light Fields

Image成像

我们了解到,成像有光栅化成像,光线追踪成像,捕捉成像(比如拍照),还有其他的成像方式

成像需要传感器

传感器上的点记录的是irradiance

Field of View视场

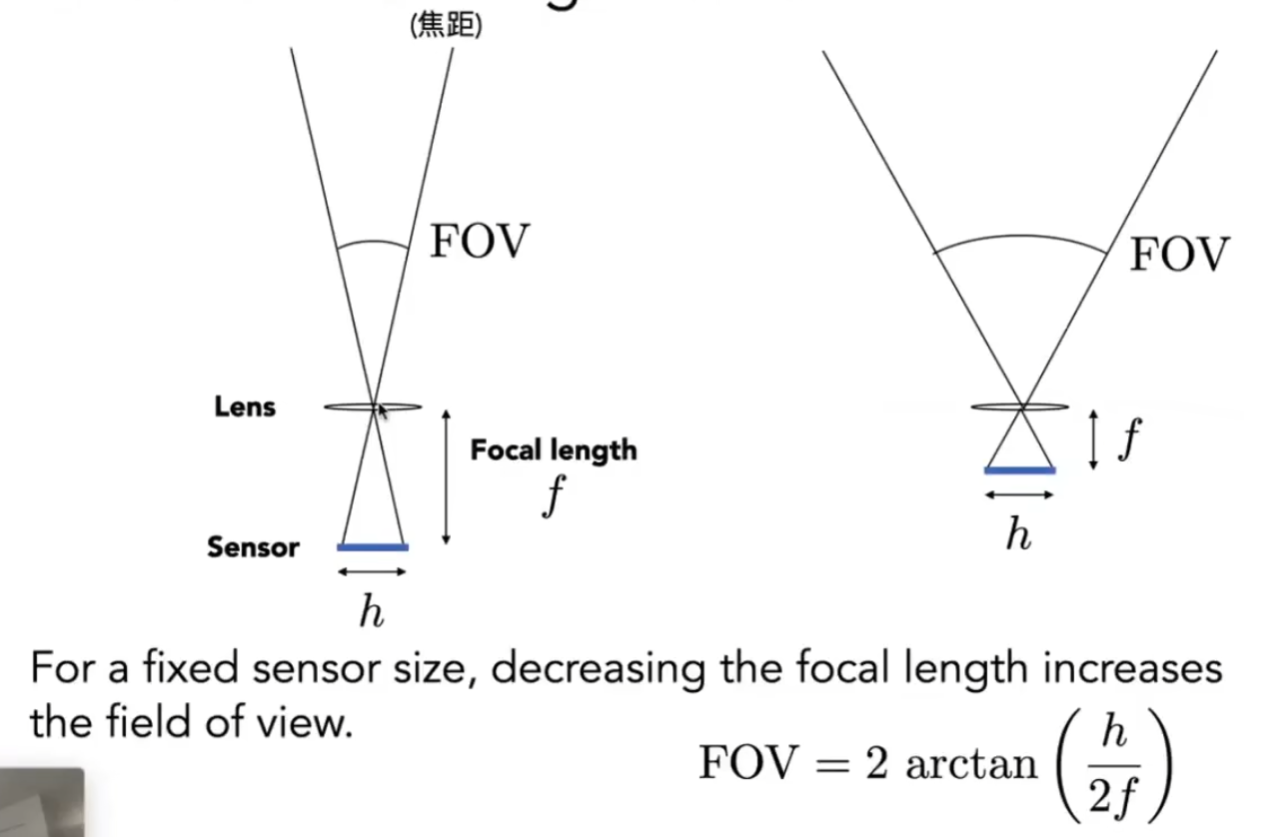
所以,增加h,减小f,就可以增大视场

Exposure曝光

决定曝光的因素,收光曝光时间和光的亮度,也就是光圈的大小,快门的时间和ISOgain感光度

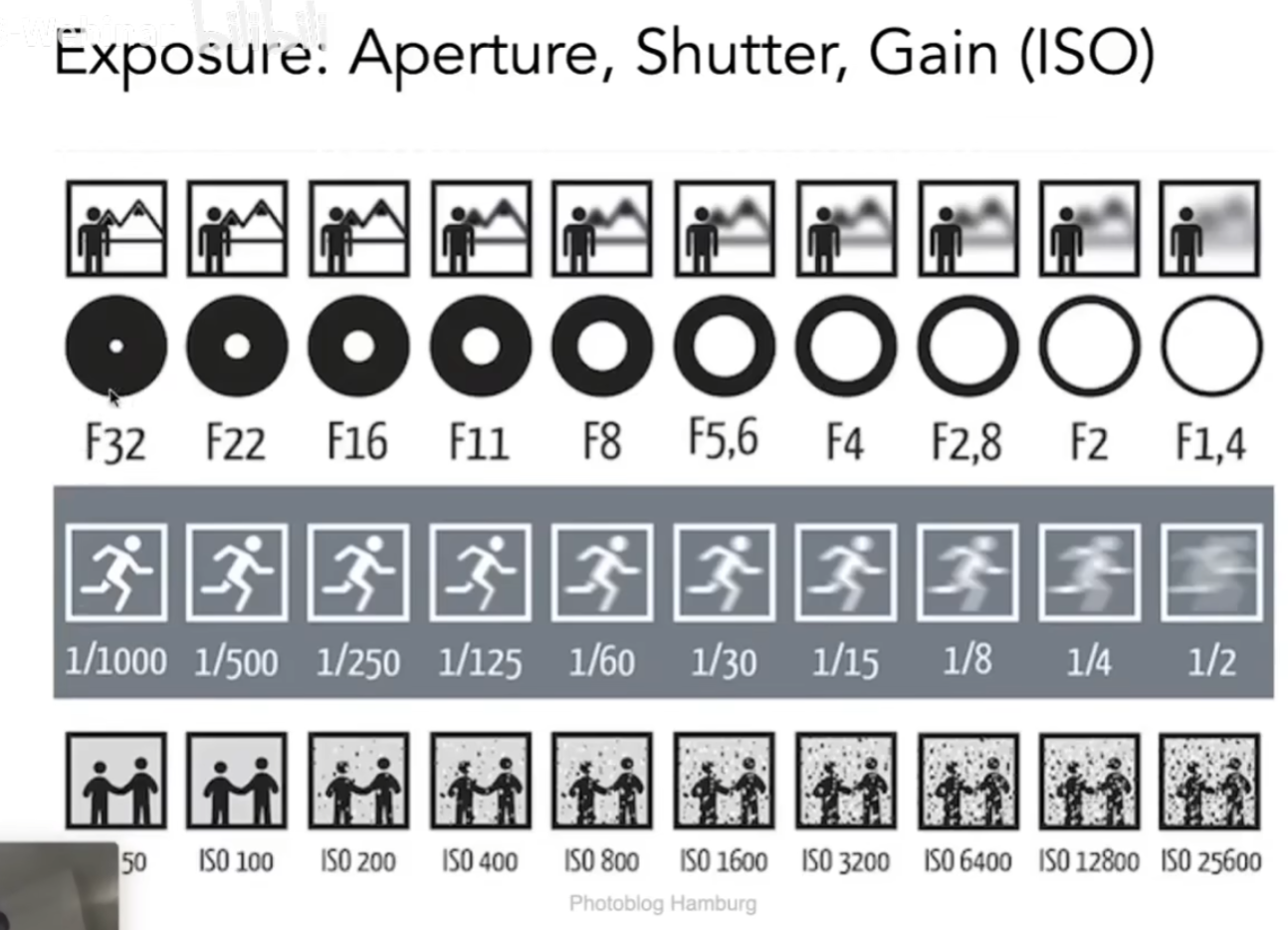
ISO

简单的放大ISO也会放大噪声

F-Number(F-Stop):Exposure Levels

用F数来描述光圈的大小,数越大光圈的直径越小

Physical Shutter

Side Effect of Shutter Speed

当相机拍摄高速运动的物体,在快门打开的时间内,物体已经产生了一定的运动,所以照片会出现运动模糊

如果减少快门的时间,会减少运动模糊,但也会减少曝光

对于速度非常快的物体,慢快门会出现Rolling shutter现象

高速摄影

用更大的光圈和ISO,很短的曝光时间

延迟摄影

用更小的光圈和ISO,很长的曝光时间

Thin Lens Approximation

对于一些真正的相机来说,镜头非常复杂

我们研究的棱镜是理想的薄棱镜,所有射入的平行光会被汇聚到一个焦点,同时我们假设这个薄棱镜可以更改焦距

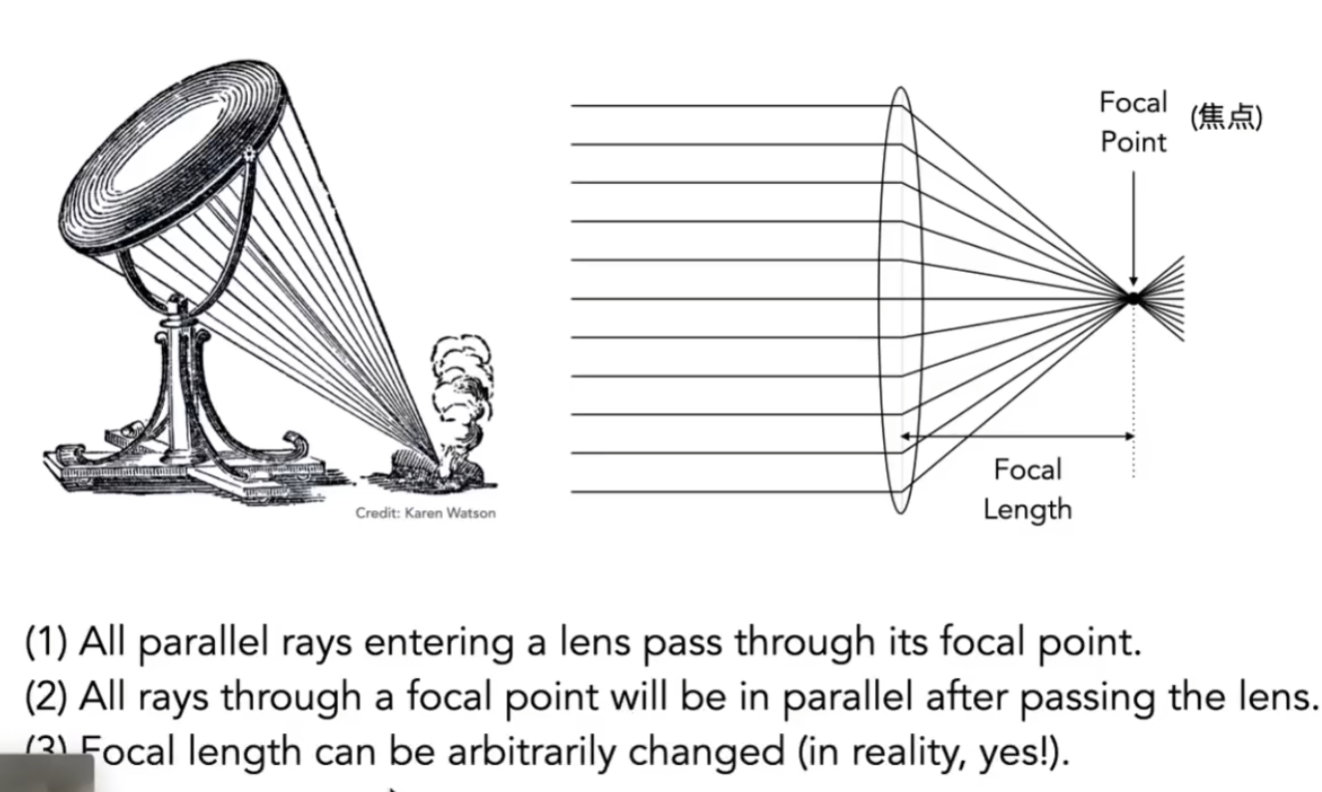
现代镜头使用的棱镜组类似上述的理想棱镜

定义焦距f,物距zi,像距zo,有以下公式


Defocus Blur

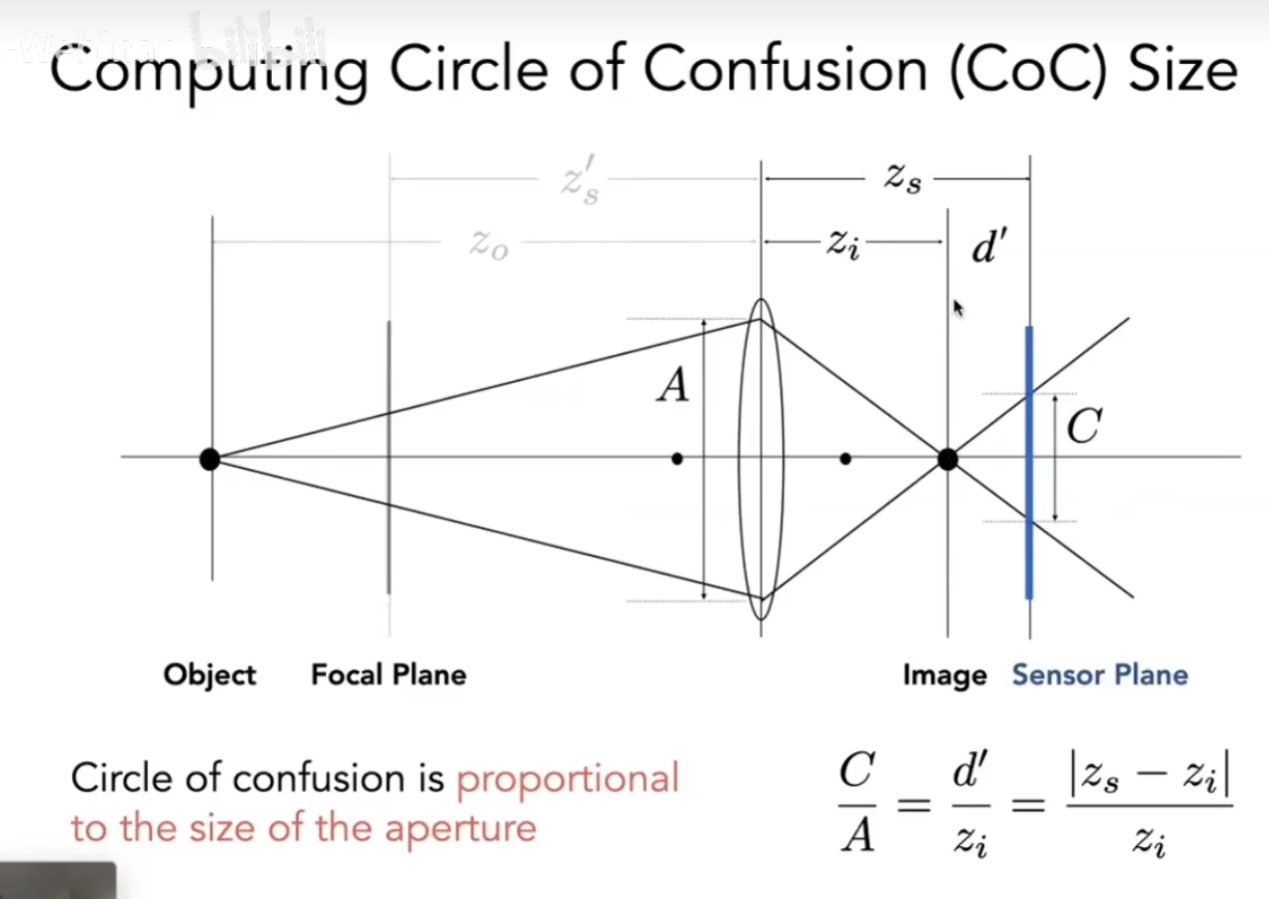
Depth of Field景深

大的光圈会得到一些模糊的图,但总归有一些地方是不模糊的,光圈的大小影响的是模糊的范围

景深指CoC足够小的范围,也是成像清晰的一段范围

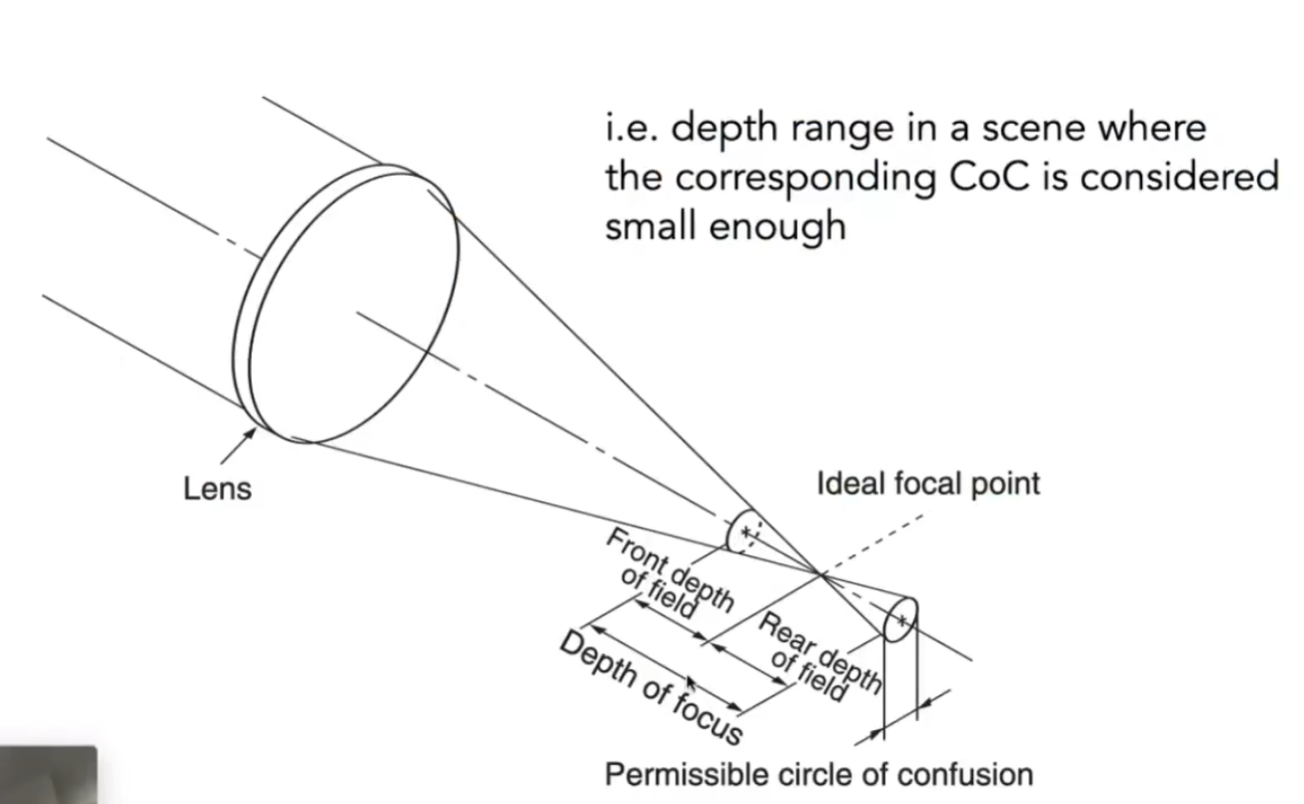
Lecutre 20:Color and Perception

Light Field/Lumigraph光场

我们从我们看到的世界是说起,如果把我们看到的东西画下来,应该是将3D的世界画成2D的图像,现在我们在面前加一个幕布,幕布上画的东西和我们刚才画的东西一样,这就是虚拟现实的原理

The Plenoptic Function全光函数

全光函数是我们能看到的所有东西,也就是在任何位置,任何方向,任何时间,看到的任何波长的光

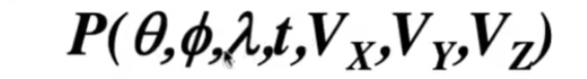
我们能看到的所有东西都可以解释成这个7维的函数

光场就是全光函数的一部分

Ray

定义一个光线,即一个起点和一个方向或两个点

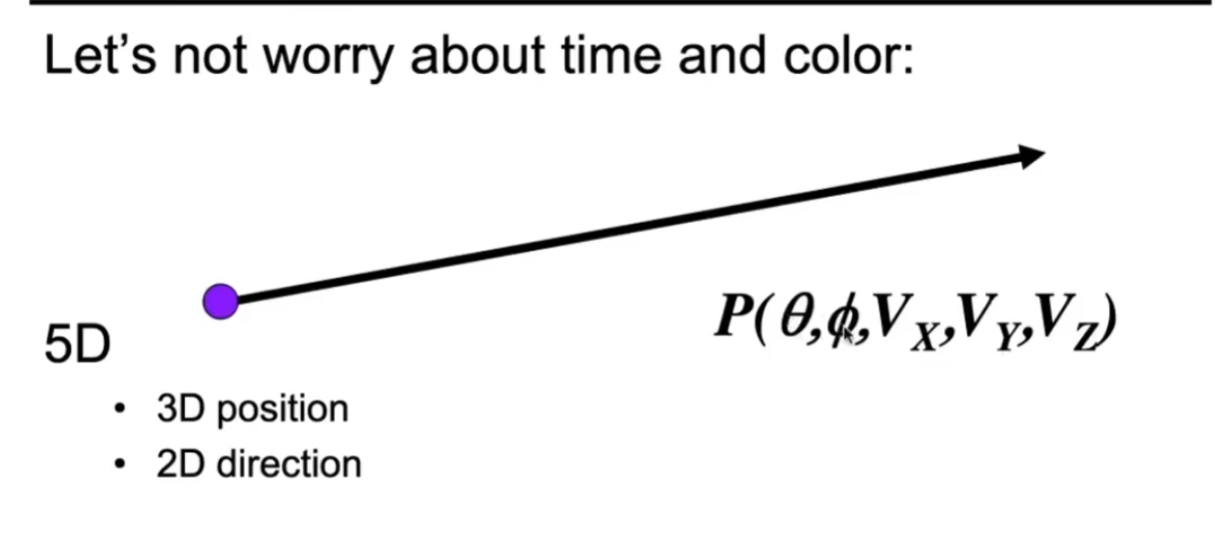
定义光场

我们不需要知道物体是什么,我们只需要知道物体的包围和在各个方向发出的光,看到光,我们就能看到物体

这些光就是光场

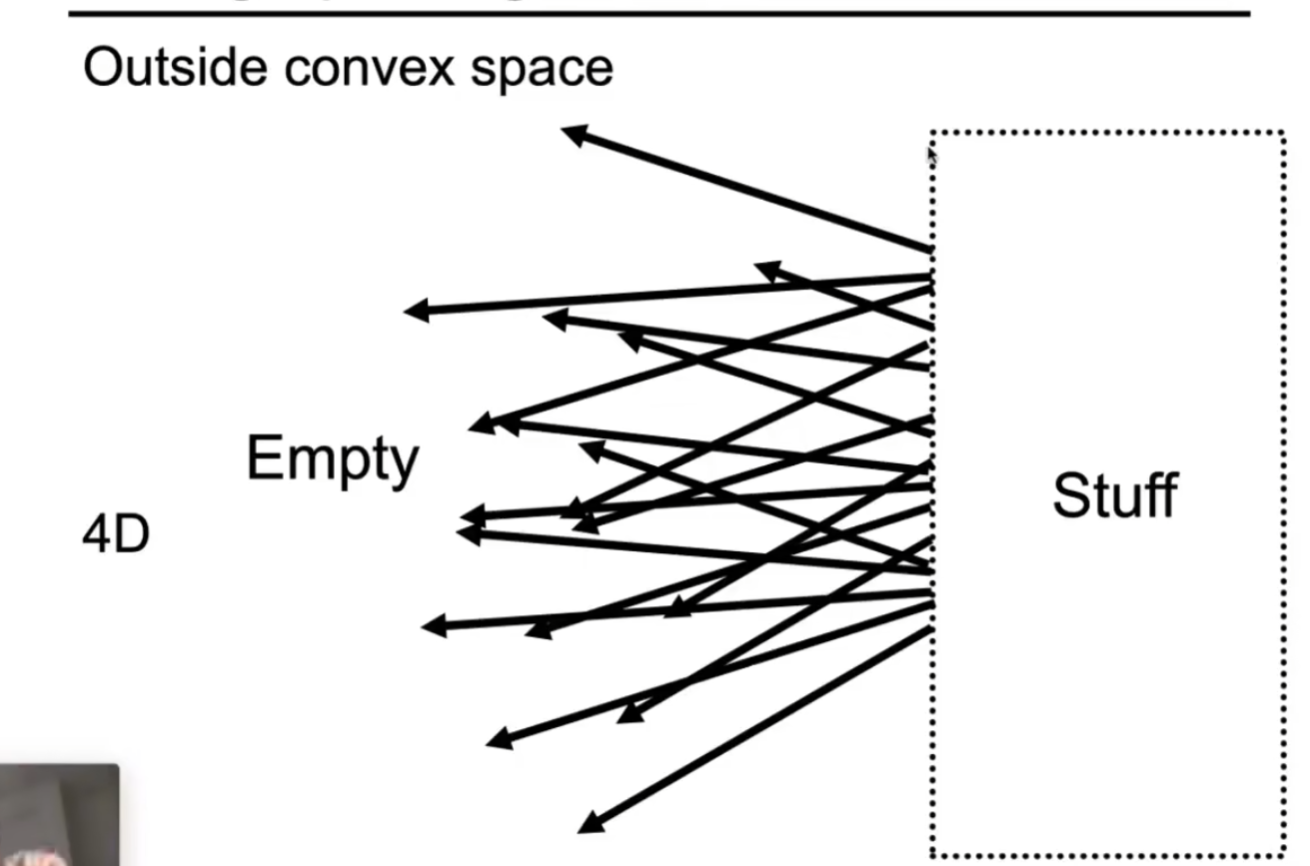
Light Field Camera

对于两个平面uv,st,一个物体在st的右边

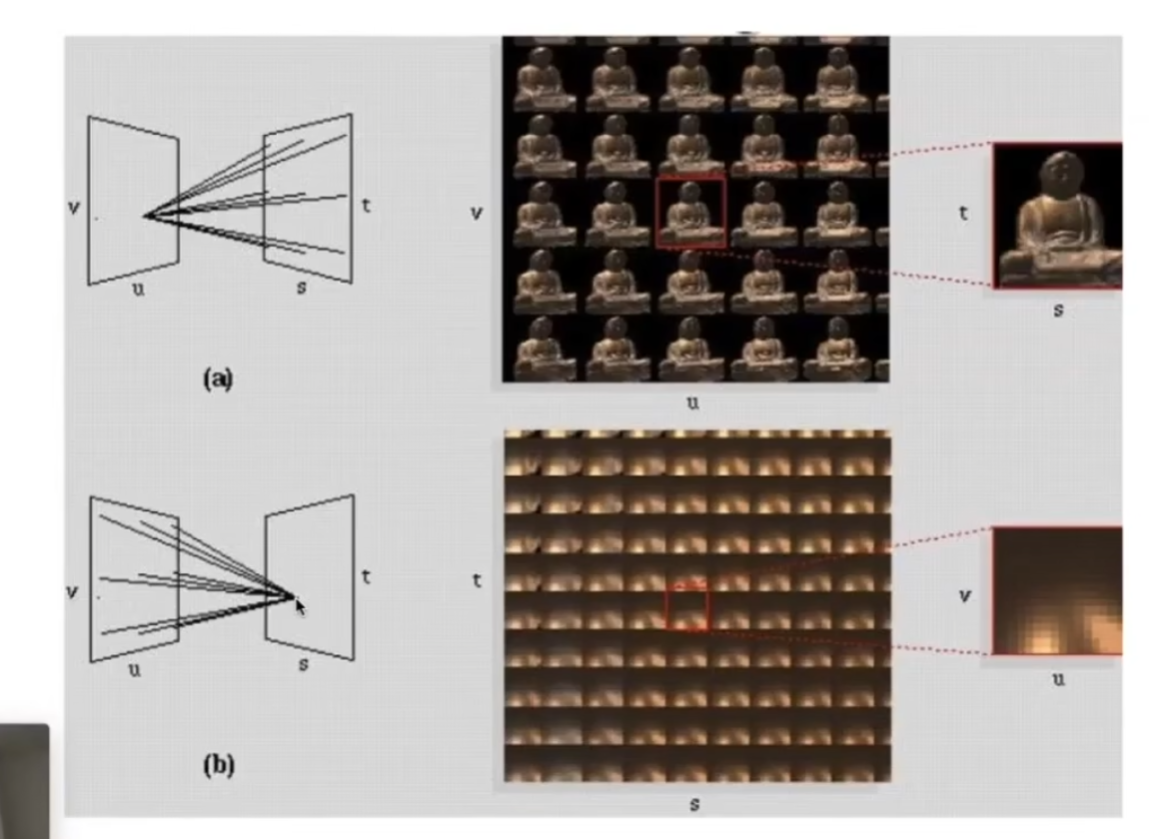
(a)表示在uv上一个点,看向st的所有方向,相当于uv上的摄像机,(b)表示在uv上所有的点,看向st上的同一点

光场照相机在各个位置记录光场

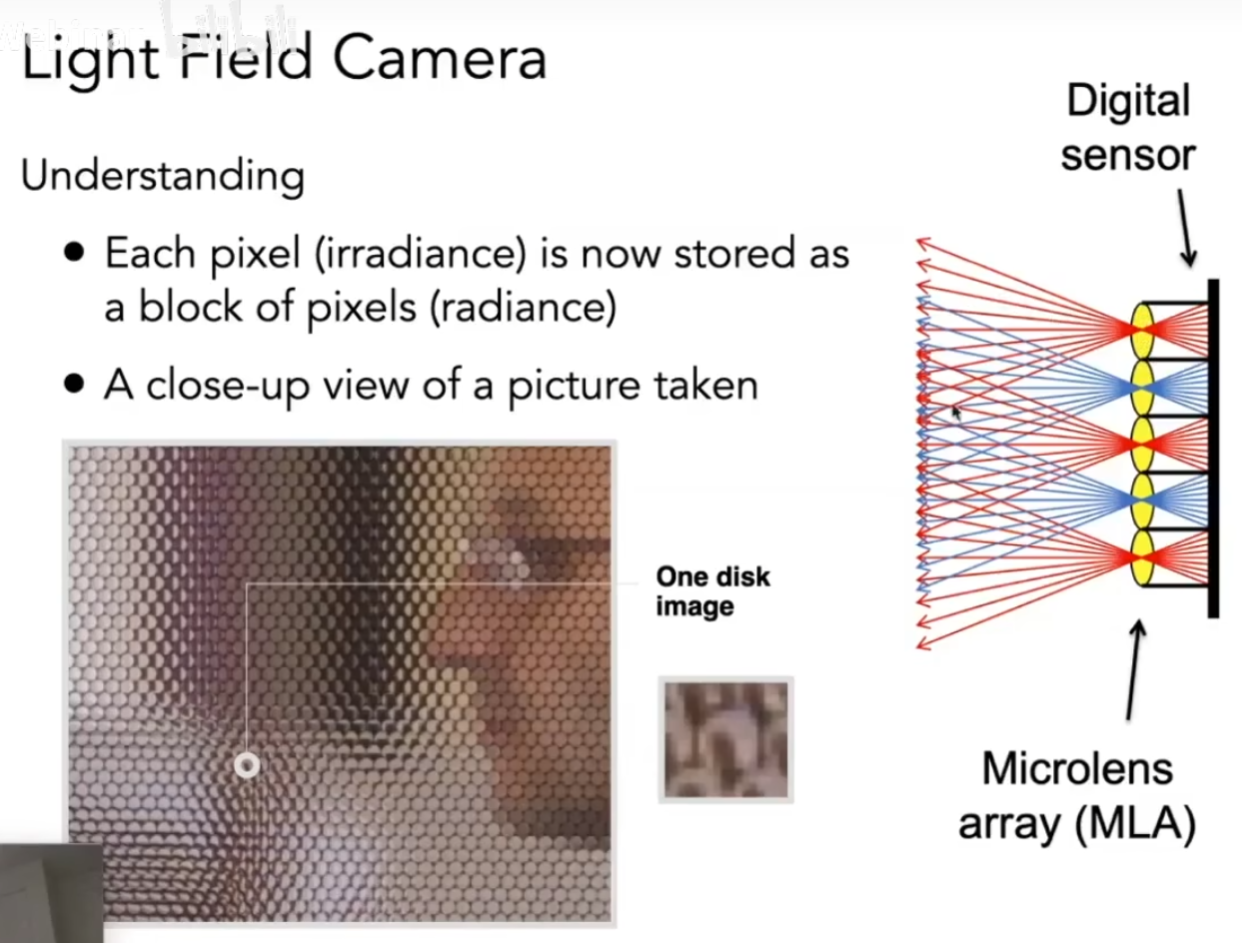
我们某一个方向的光,就可以得到一个照片

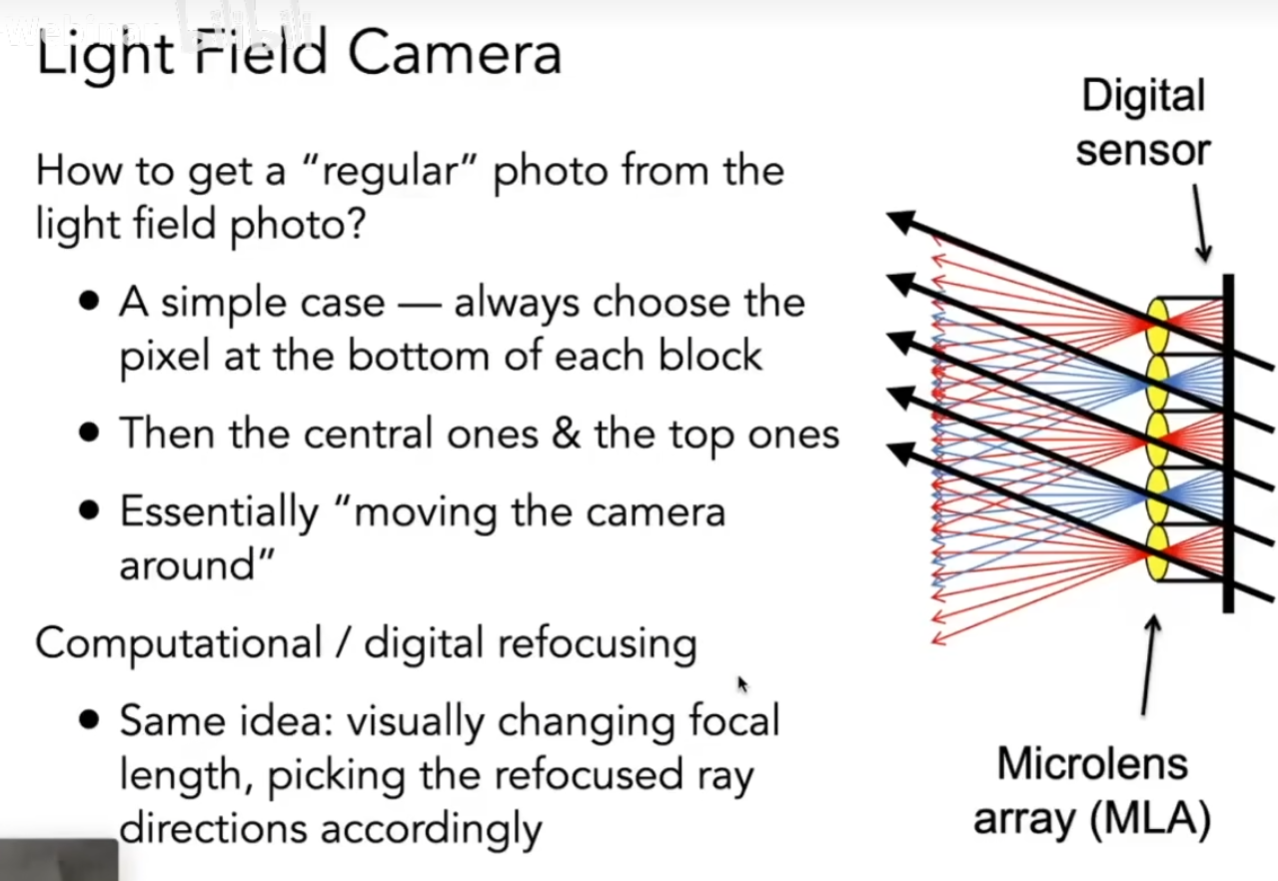
通过取不同方向的光,我们就可以在拍过照之后”移动”相机的位置

Color

颜色与光有关,或者说与光的光谱有关,图形学关心的是可见光的光谱

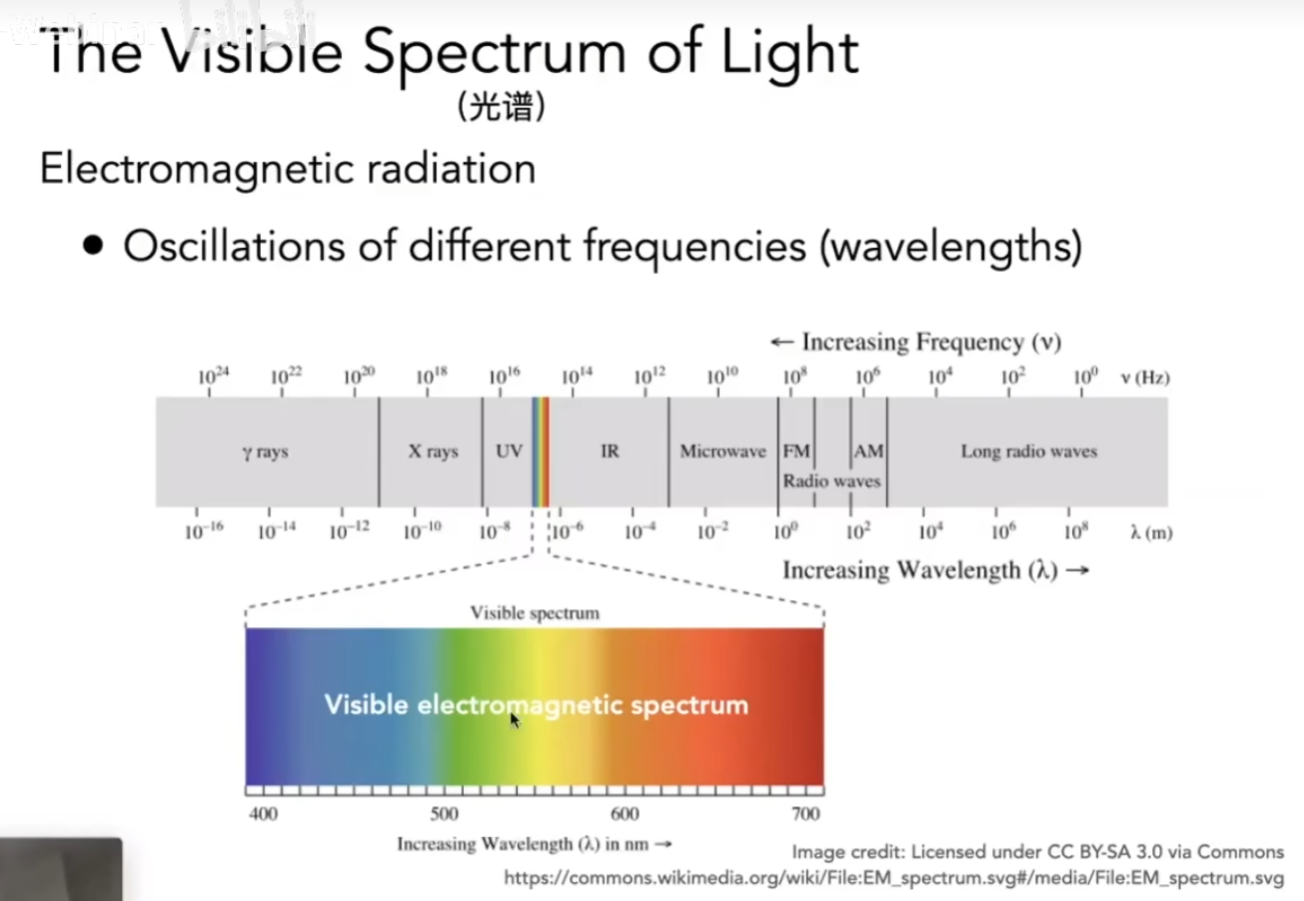
那么什么是颜色呢

颜色是人的感知

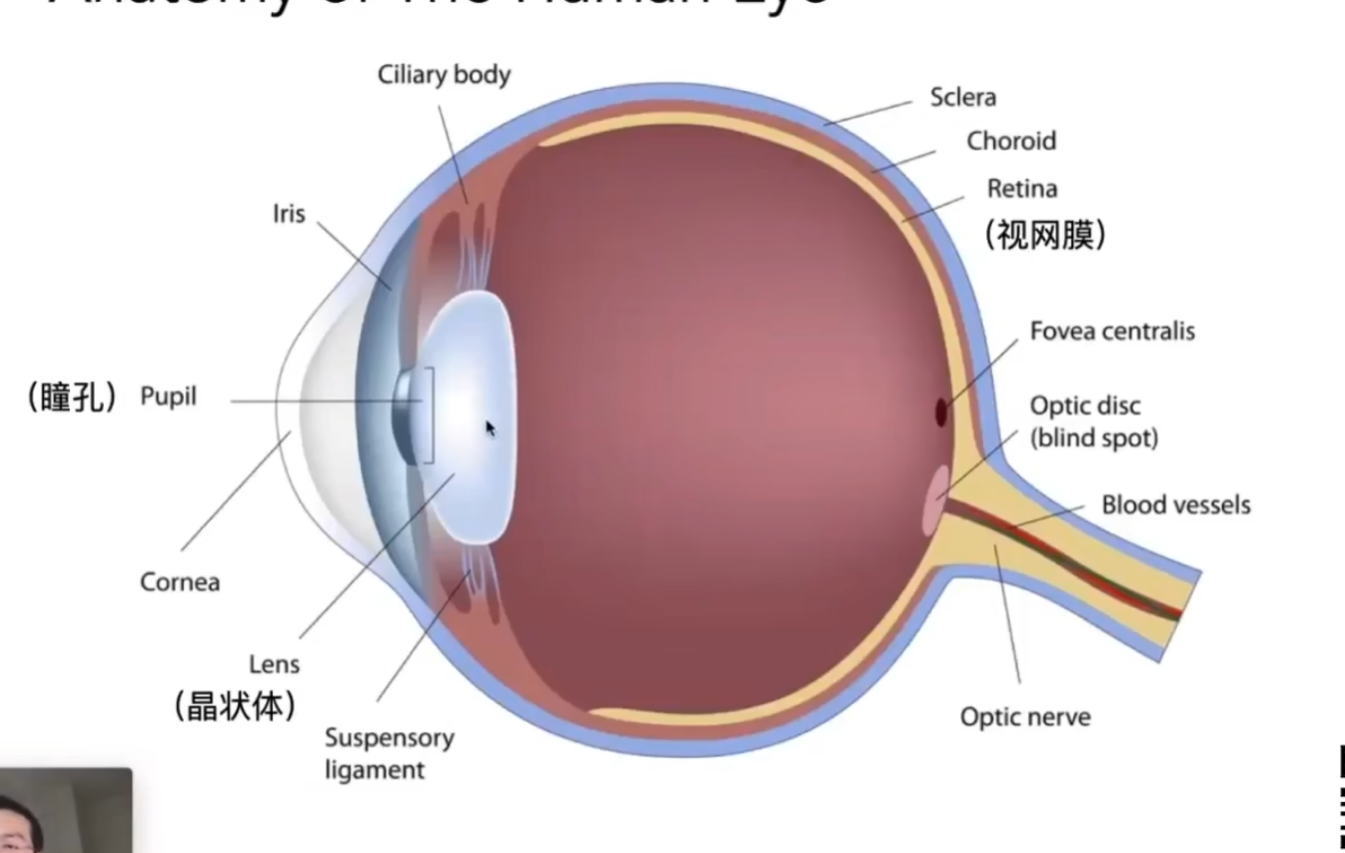
人眼上有锥形细胞,用于感受光的强度

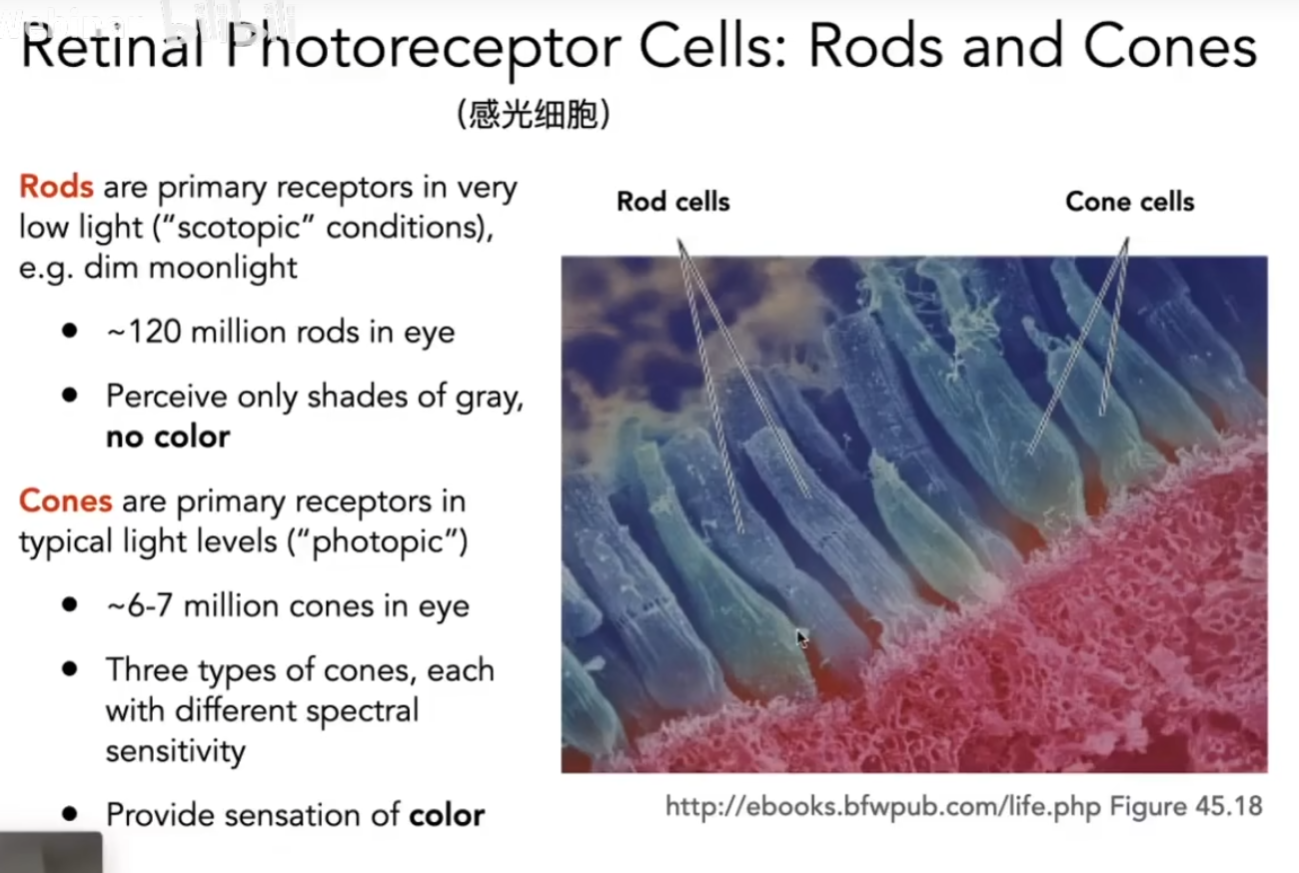
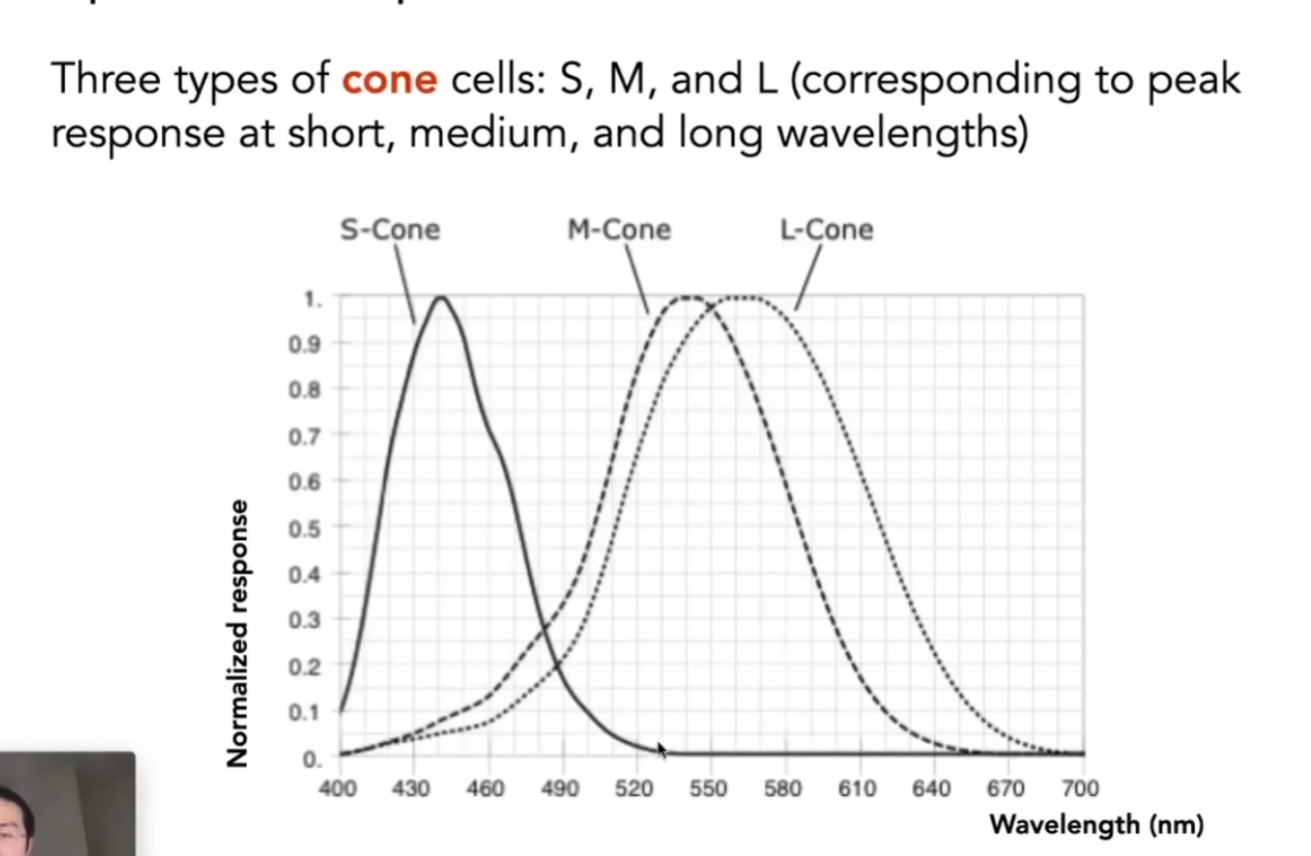
锥形细胞有三种,S,M,L三种细胞能感受波长不同的光

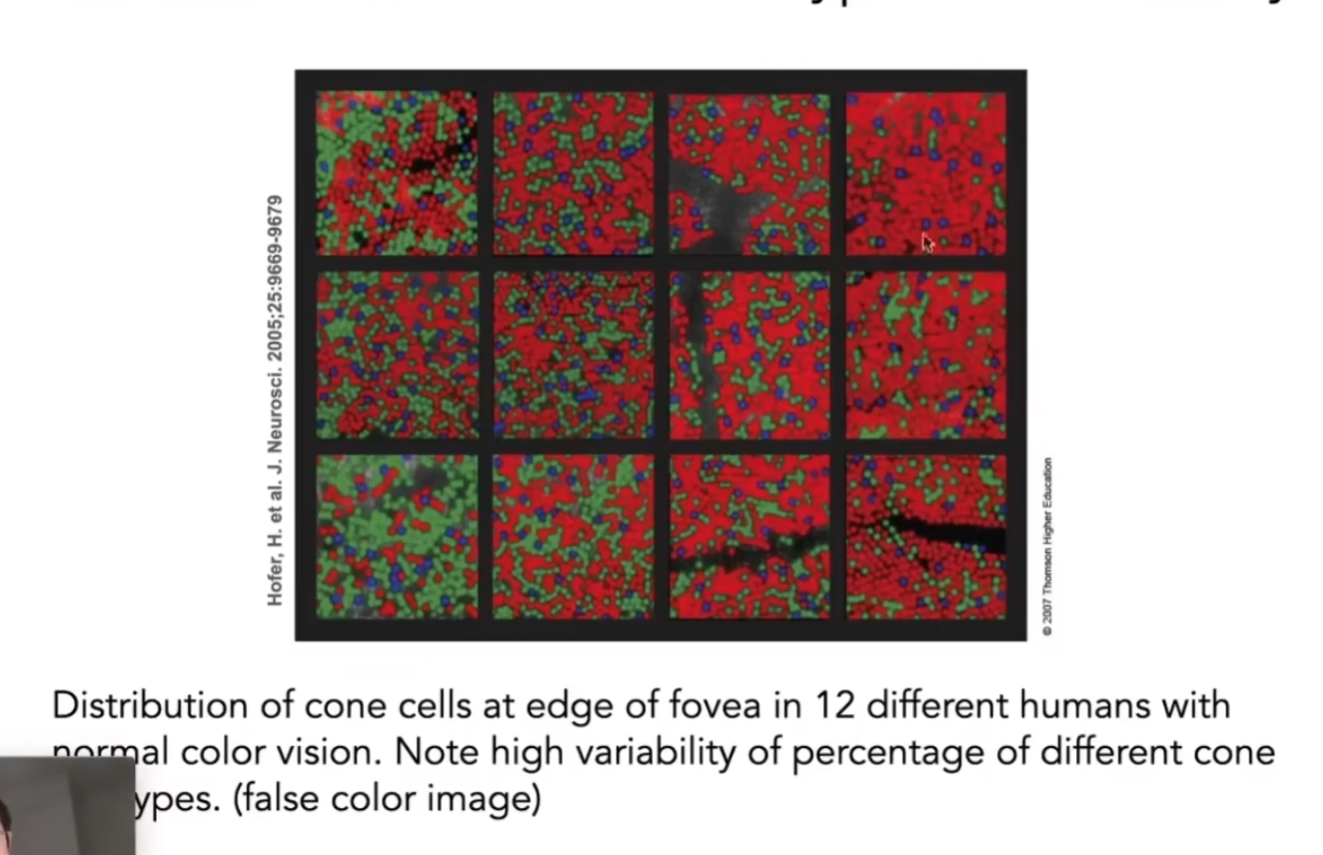
不同的人眼中的三种细胞的分布,非常不一样,以下12张图来自12个人

这三个细胞会得到三个数,大脑看到的不是光谱,而是三个数

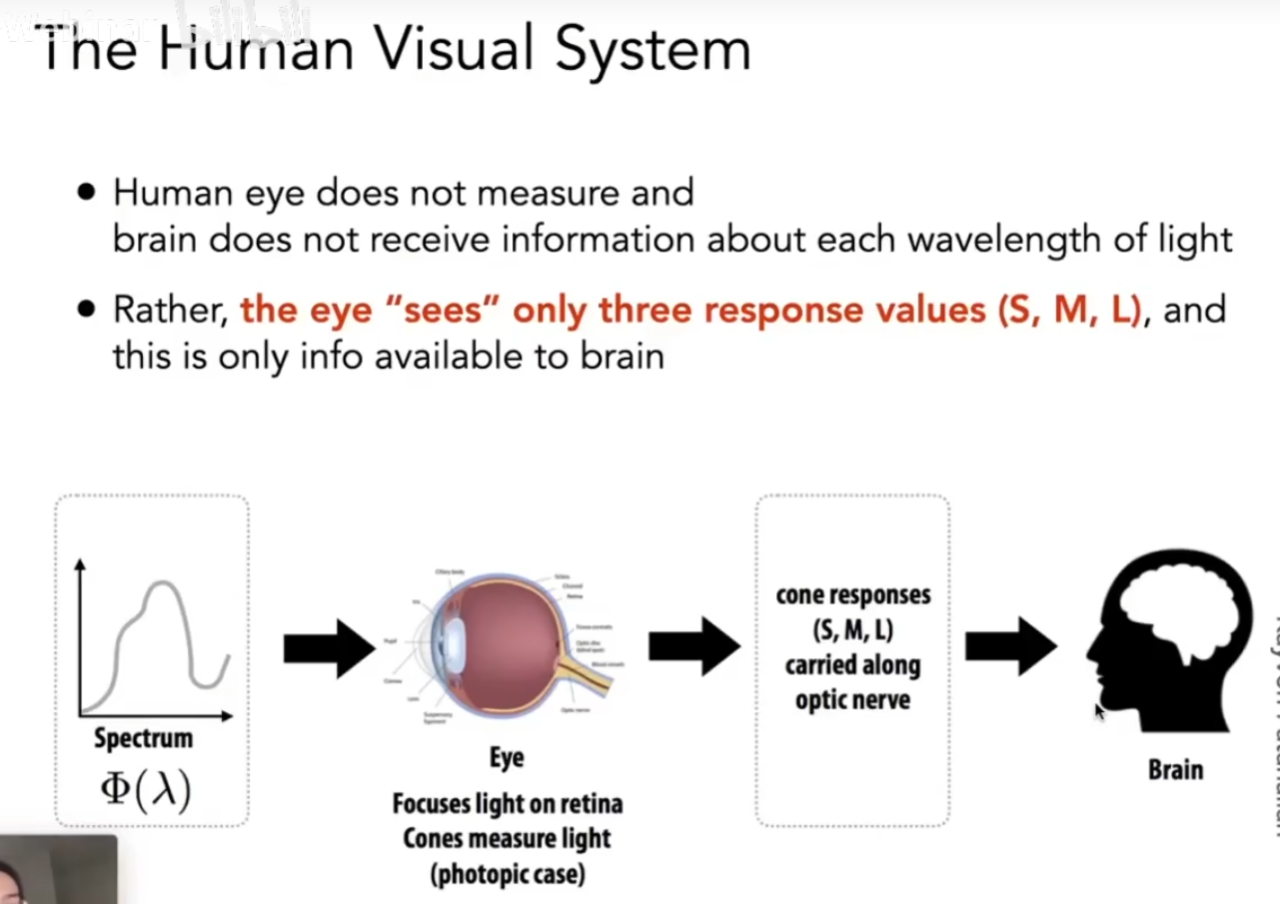
同色异谱现象

有可能会出现光谱不同,但锥形细胞得到的数相同的情况

加色系统

以最常见的RGB为例

加色系统允许我们将颜色线性相加

加色系统的所有颜色相加是白色

Color Spaces

sRGB是广泛使用的颜色空间

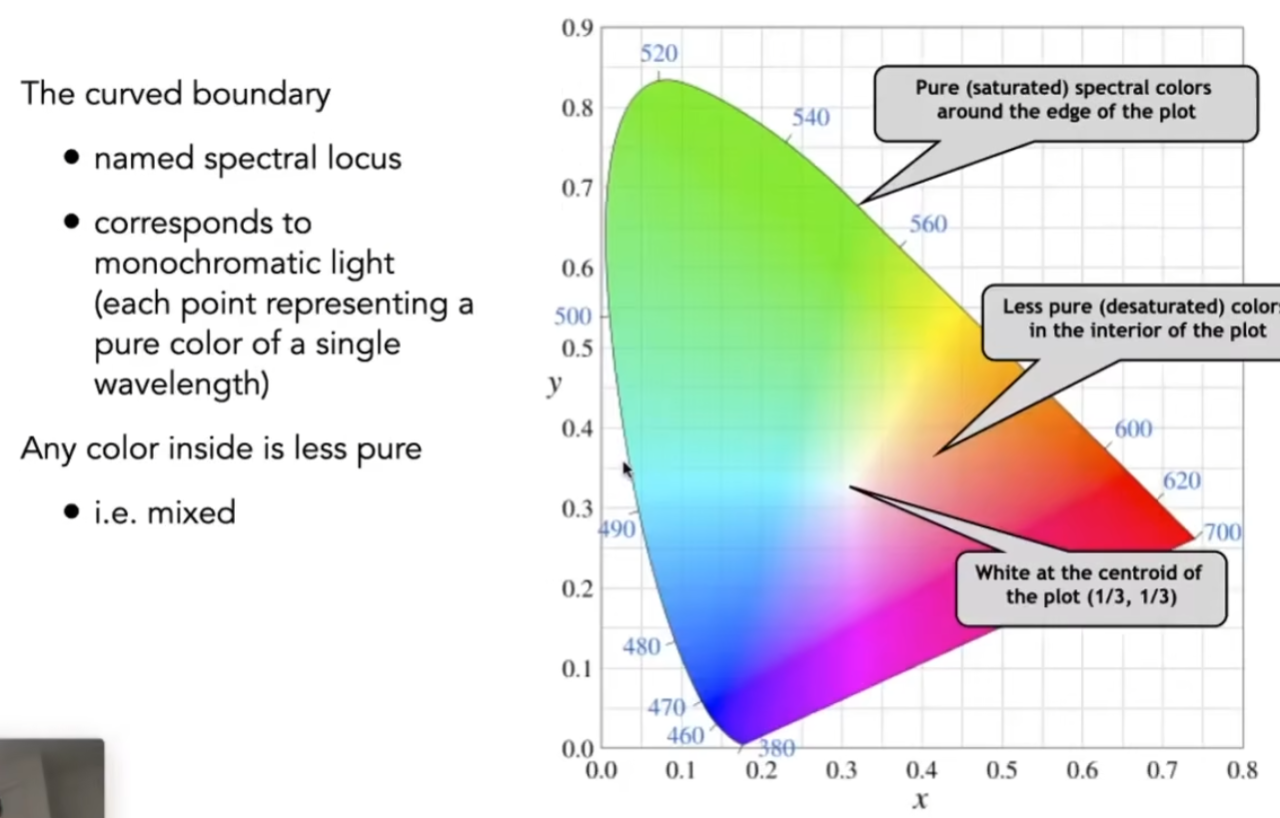
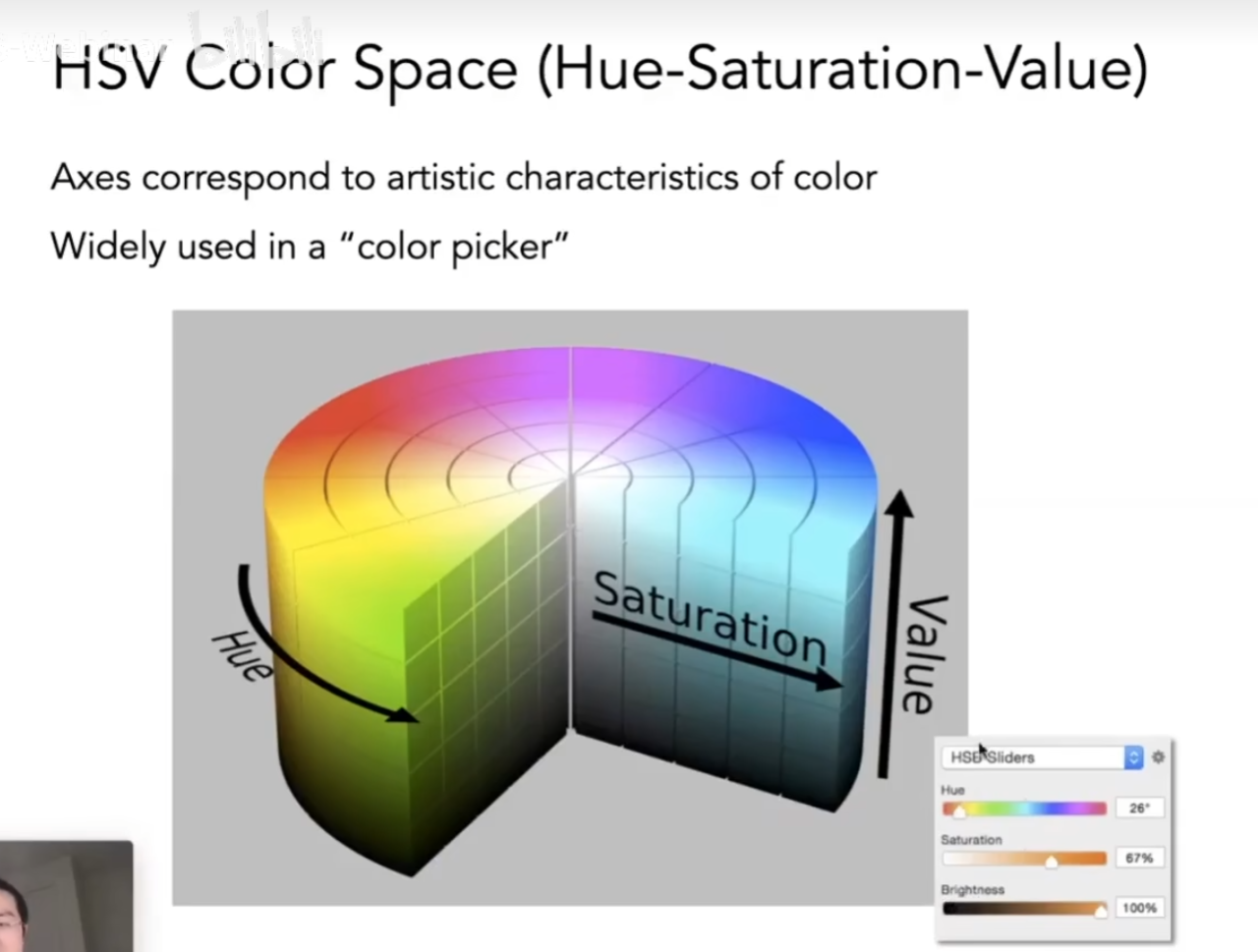
还有别的颜色空间,比如HSV

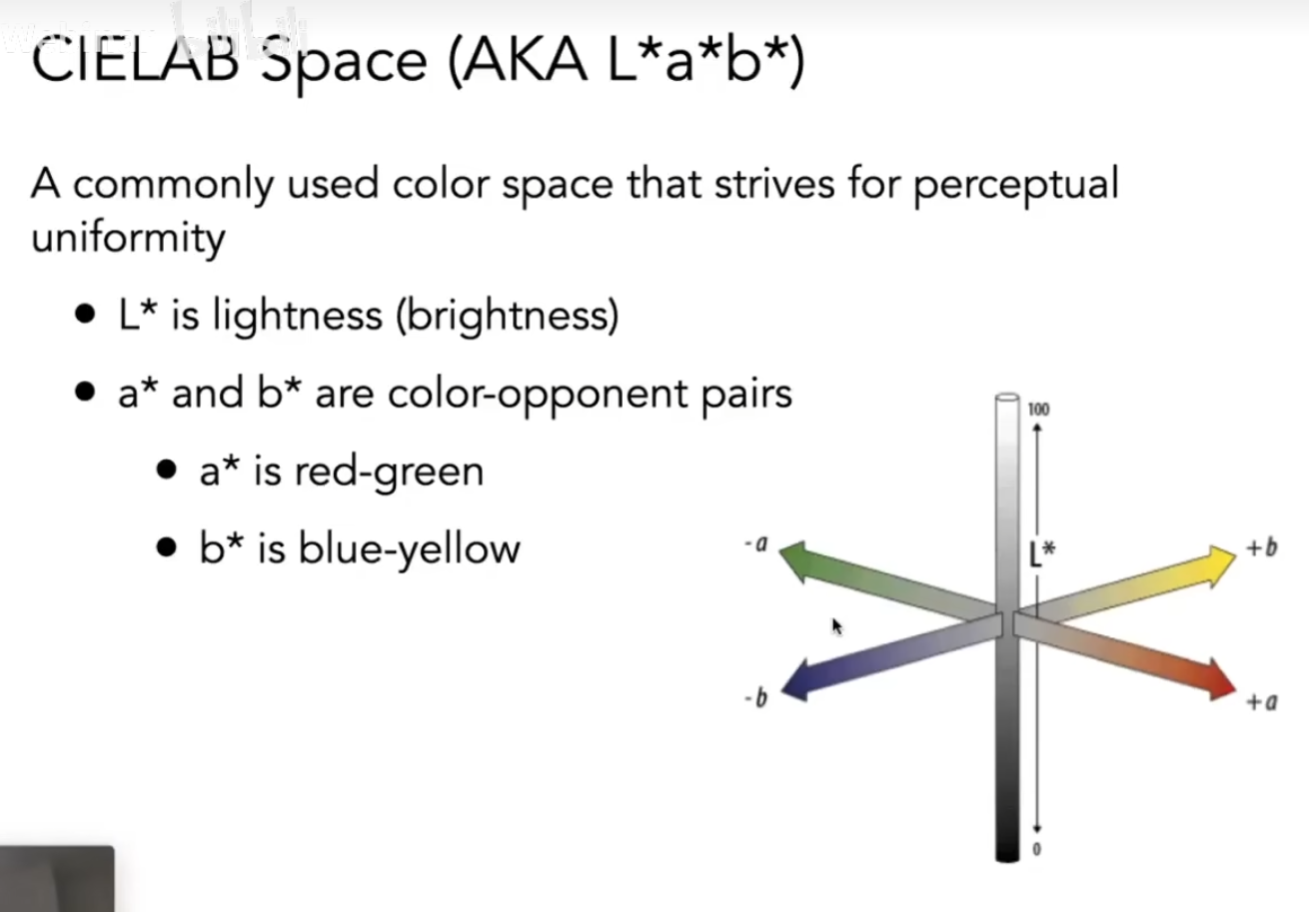
以及CIE

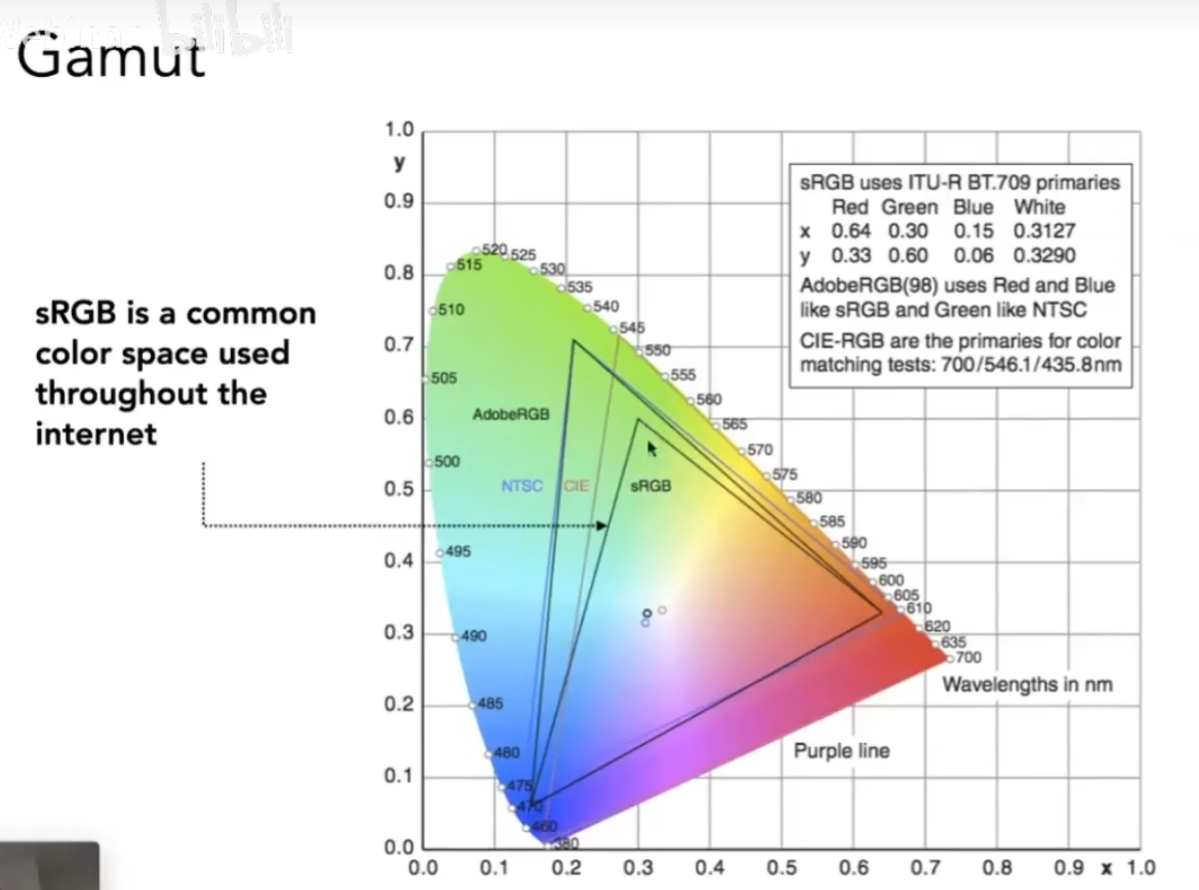
Gamut色域

色域是一个颜色空间能表示的所有颜色

减色系统

以CMYK系统为例

减色系统的所有颜色相加是黑色

Lecture 21:Animation

Keyframe Animation关键帧动画

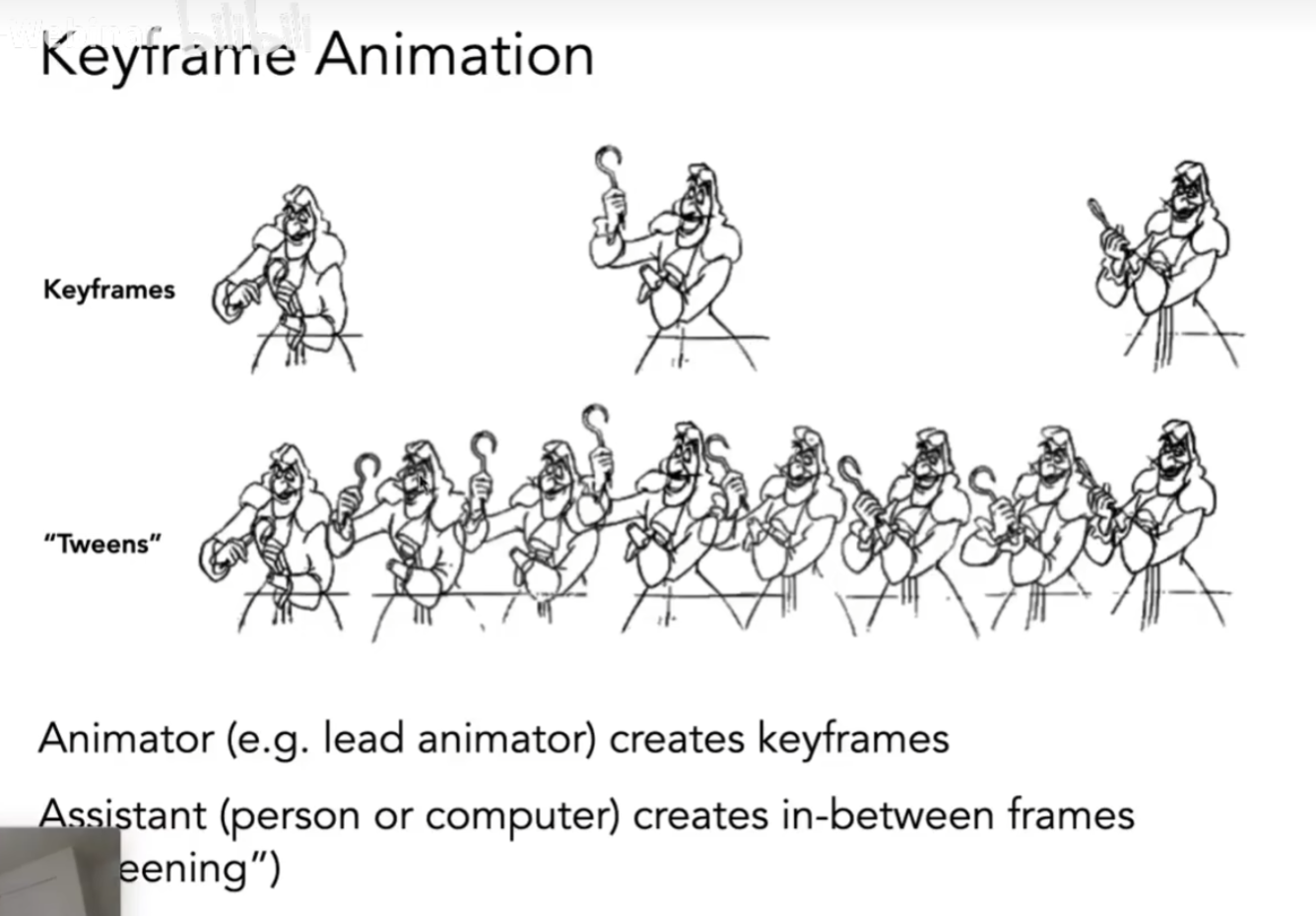
我们有了这些关键帧后,帧与帧之间的部分可以差值补充

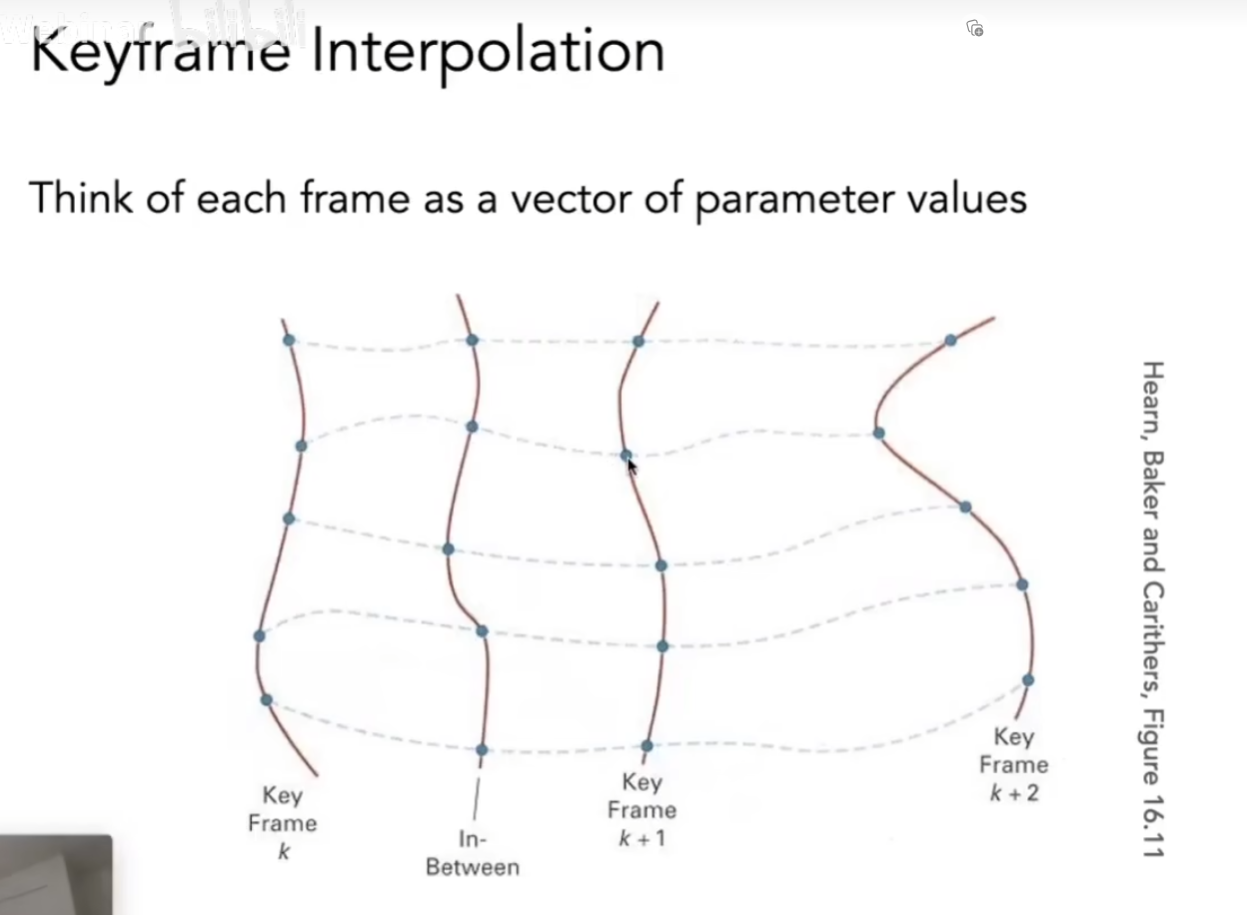
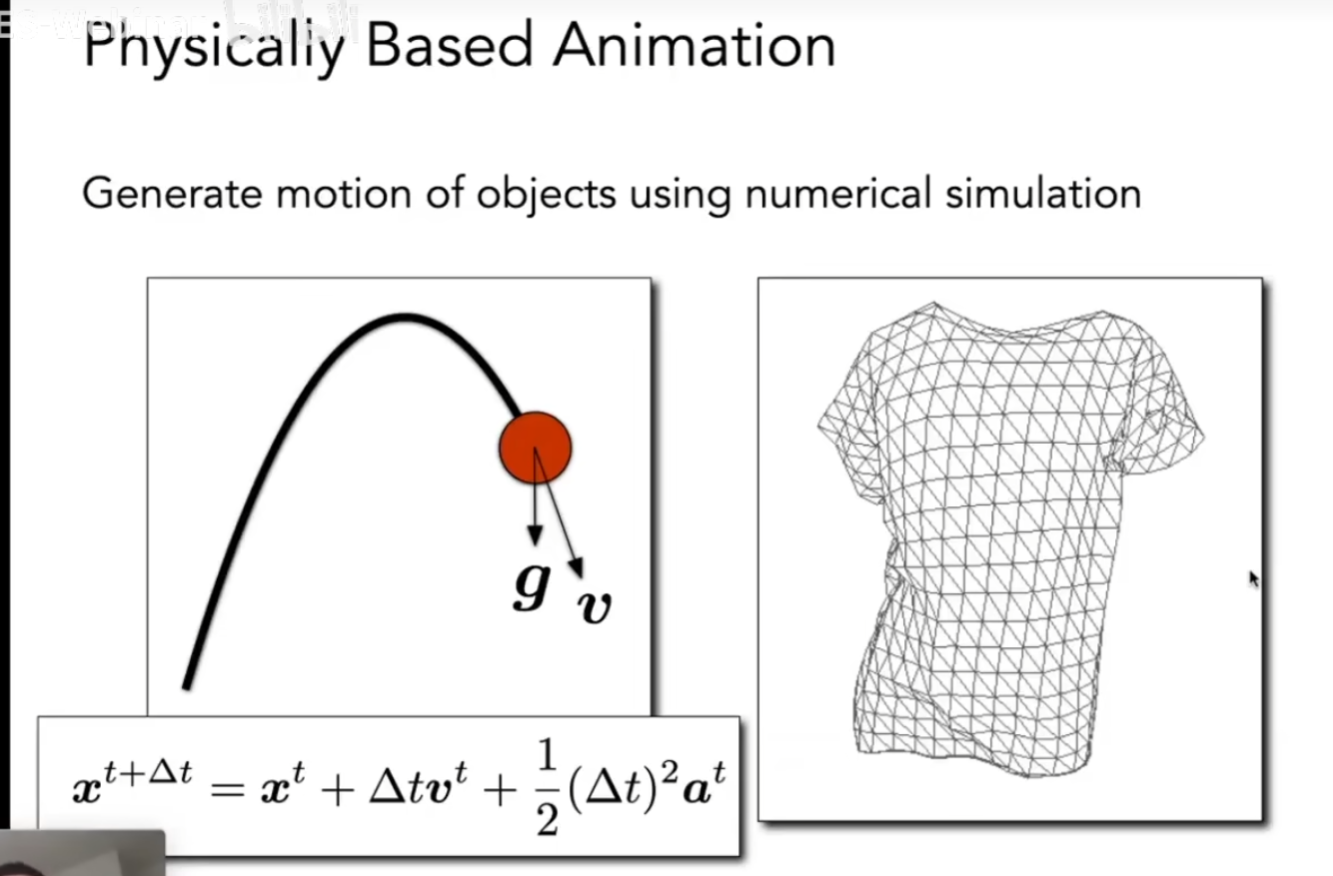
Physical Simulation物理仿真

如果我们知道物体此时收到的力,或者运动趋势,我们就可以知道物体下一帧的位置和形态

Mass Spring System质点弹簧系统

质点弹簧系统是一系列相互连接的弹簧和质点

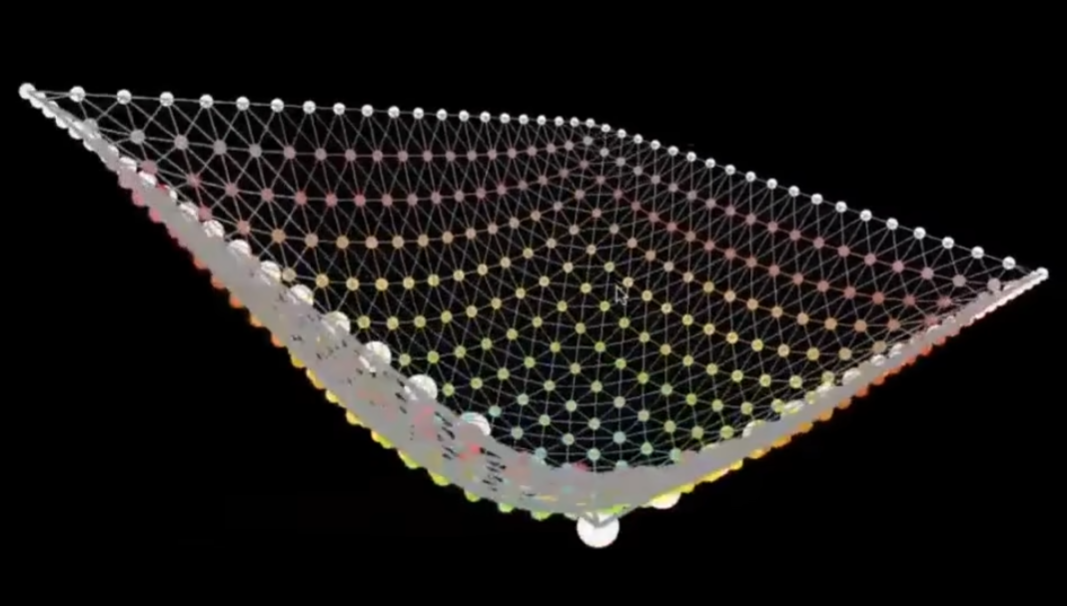
理想的弹簧遵守胡克定律且长度为0

但弹簧应该有一定的长度

如果给理想弹簧施加过一个力,弹簧会一直震动,所以我们需要给弹簧施加”摩擦力”

这个弹簧的作用应该是将弹簧最终恢复为未拉伸的状态

Particle System粒子系统

Forward Kinematics运动学

我们可以定义三种不同的关节,Pin,Ball,Prismatic joint,用关节来控制物体的运动

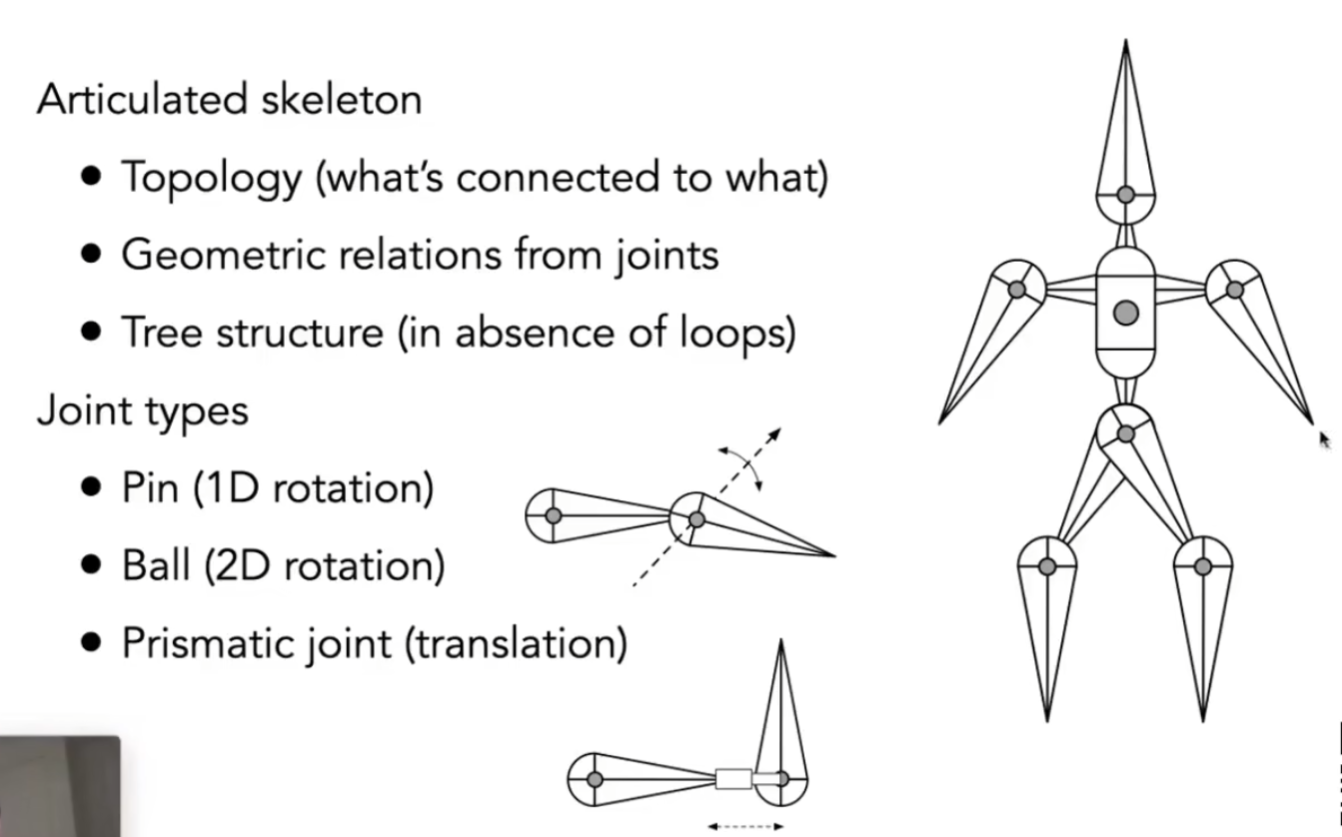
给定物体移动的角度,我们就可以得到物体的位置

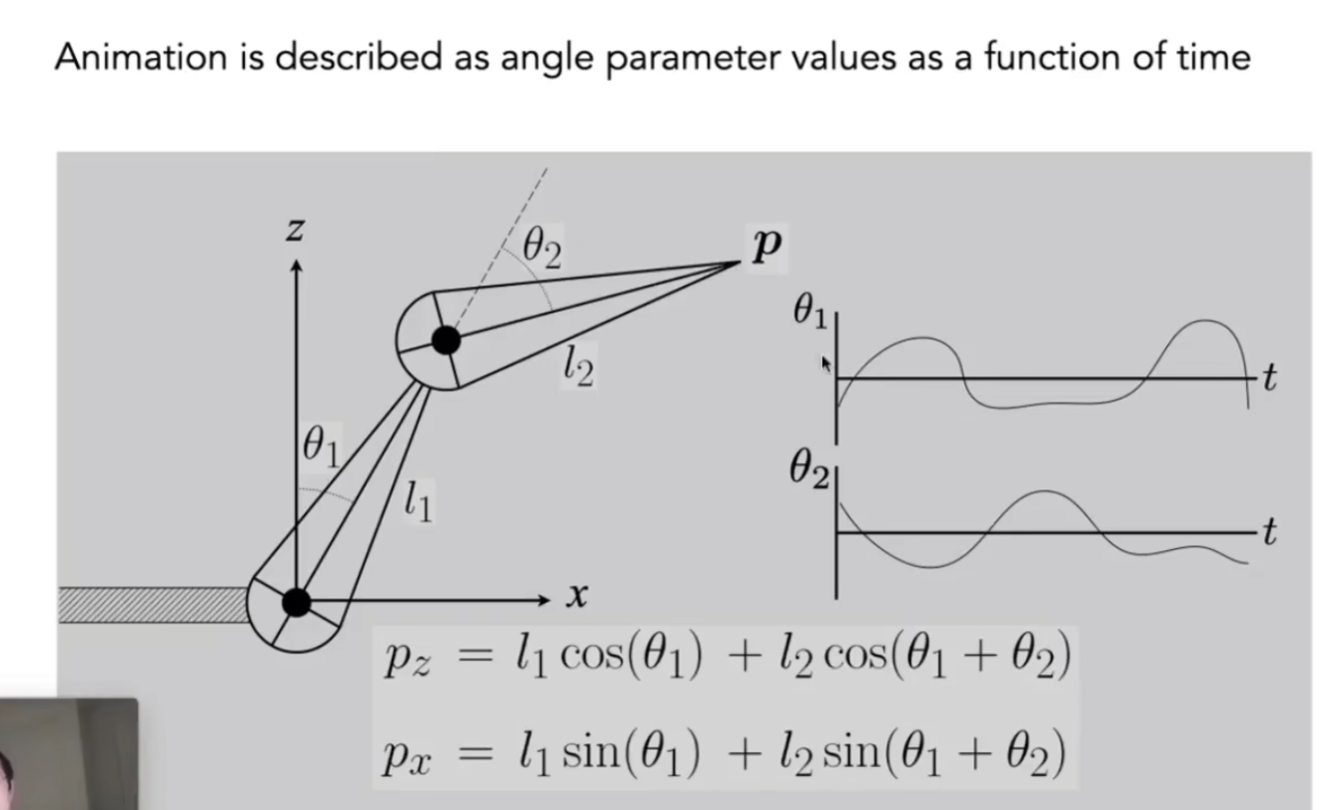
为了让艺术家更轻松的使用关节,可以使用逆运动学

Inverse Kinematics逆运动学

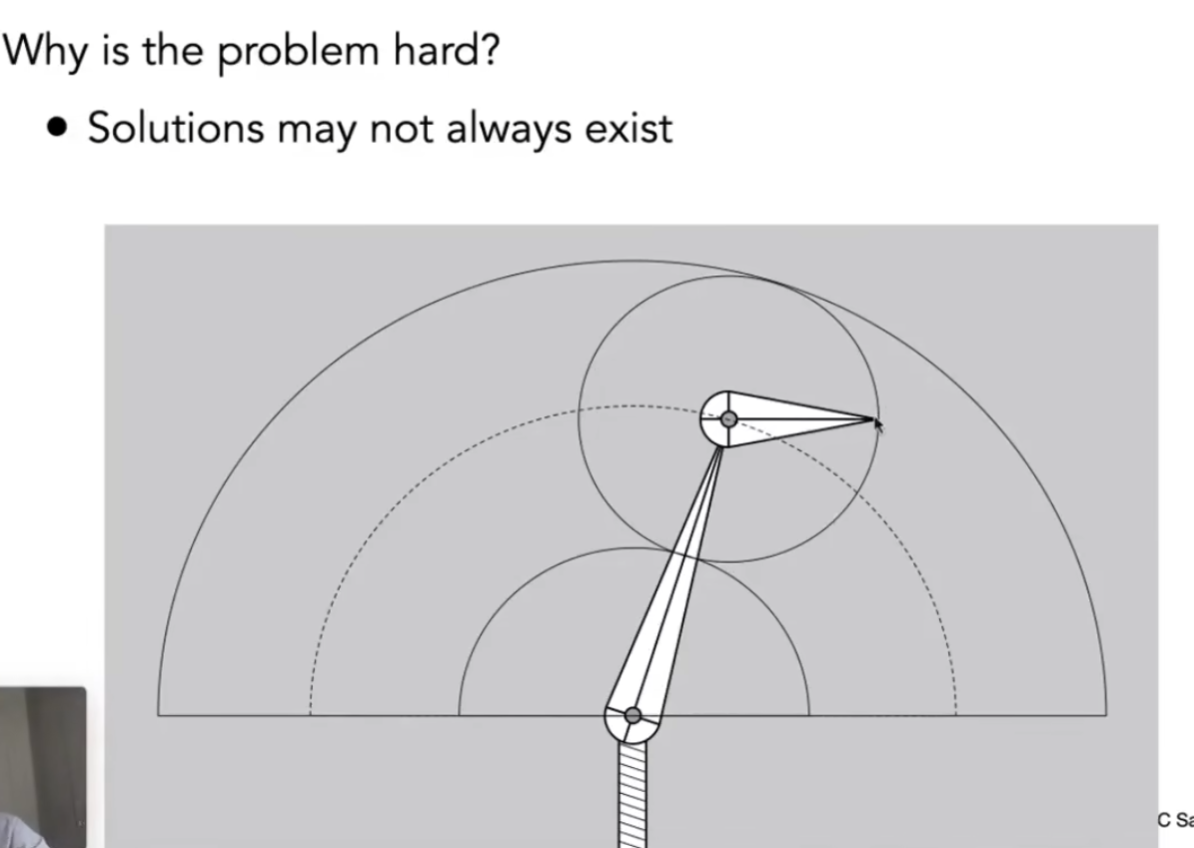
给定物体将移动的位置,就可以得到物体在运动中旋转的角度

但物体的位置移动很可能出现多解或无解

Rigging骨骼绑定

Blend Shapes

如果已经有了物体的两个形态,可以将两个形态的控制点差值,得到中间的形态

Motion Capture动作捕捉

用控制点将真人的动作反映到虚拟的物体上

Lecture 22:Animation (cont.)

Single Particle Simulation

我们希望在速度场中模拟粒子的移动

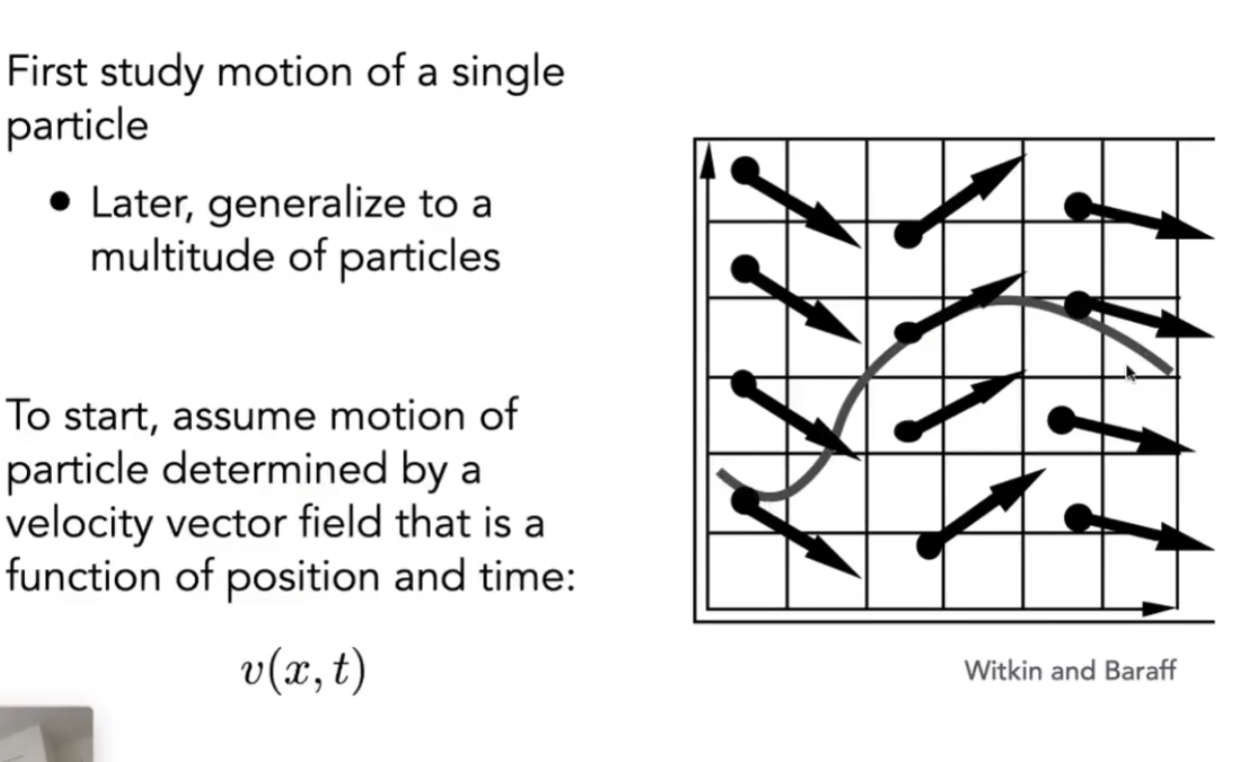
使用欧拉方法

上一个时刻有一个位置和加速度,下一个时刻位置就可以是上一时刻的位置加上位移

也就是说,我们始终用上一帧的量,推测下一帧的量

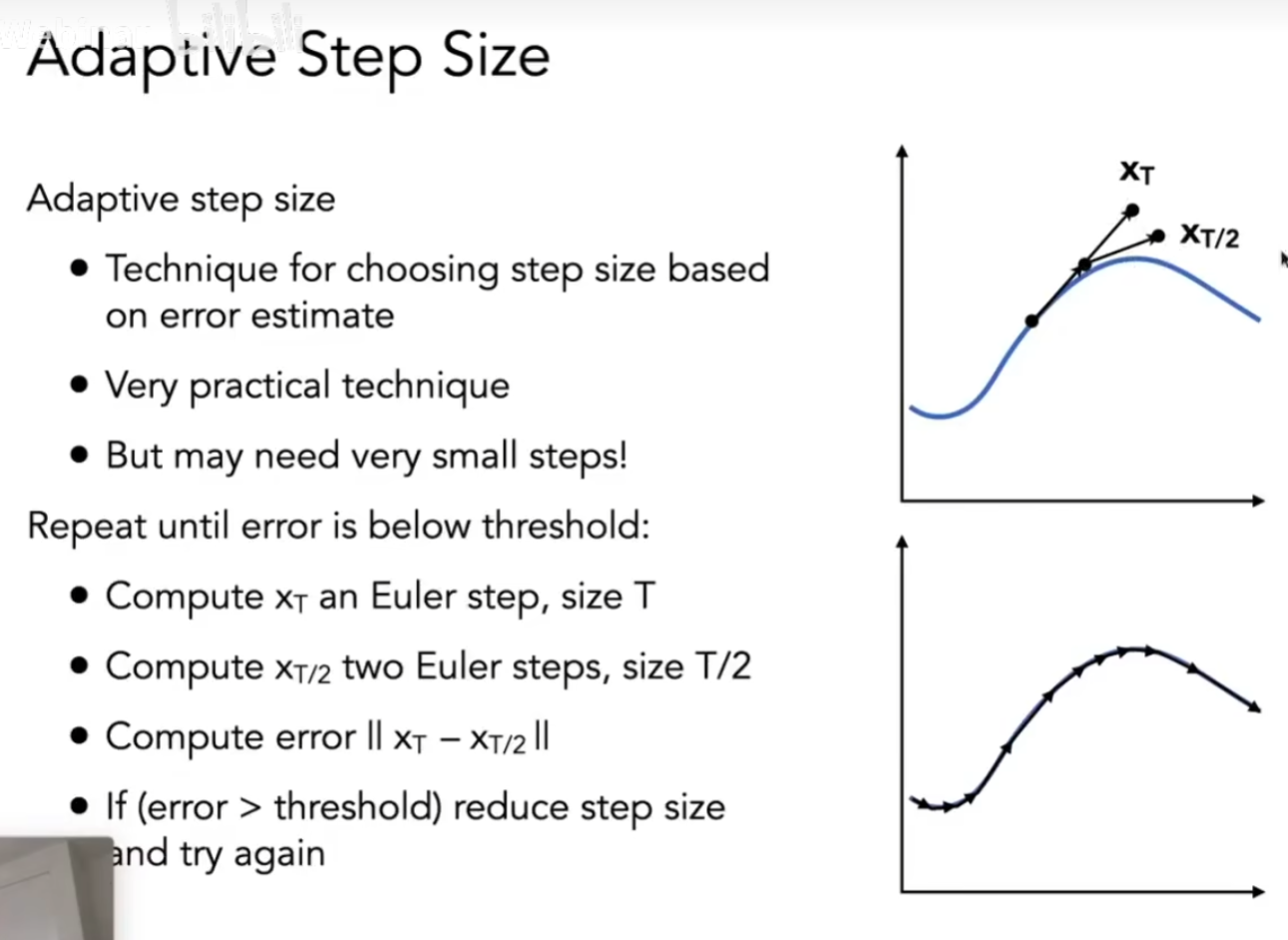
但使用欧拉方法会很不稳定

如果我们使用的t太长,就会出现较大的误差,粒子在某些速度场中会出现很大的位置错误

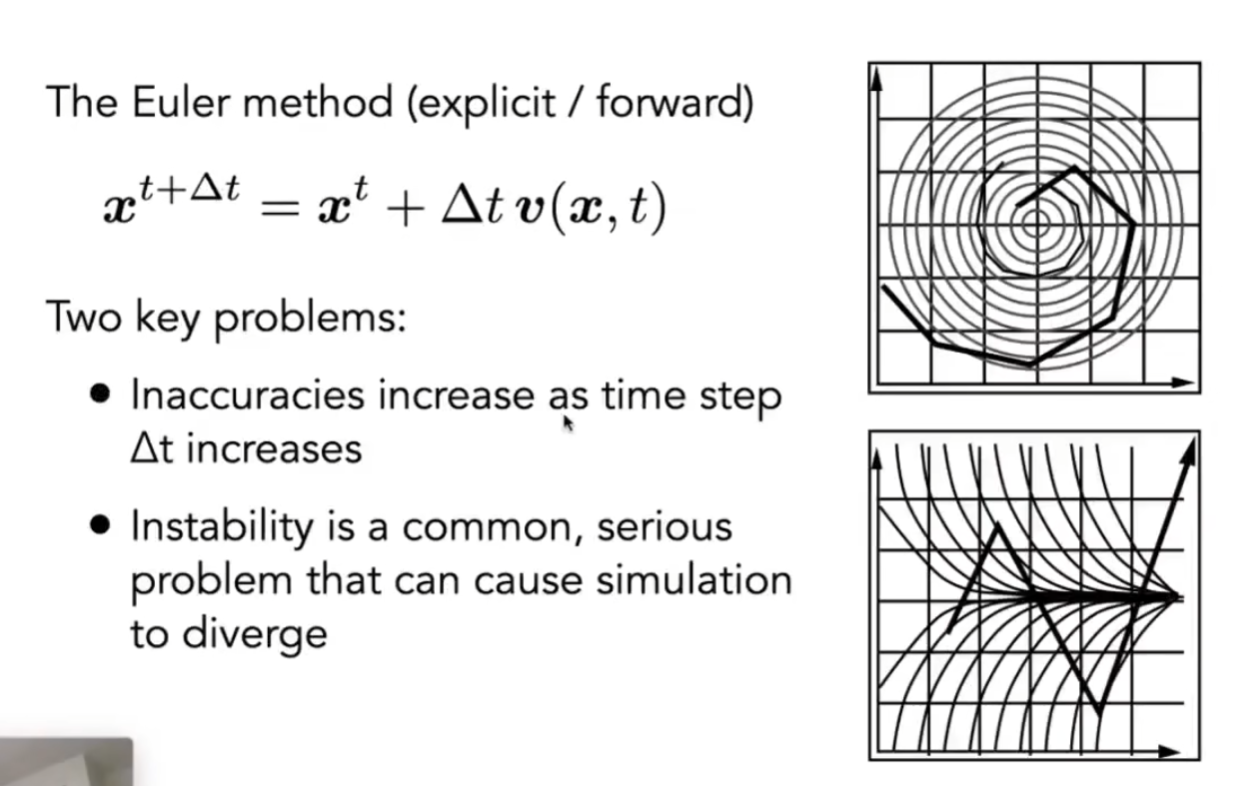
Midpoint Method

如果我们有一个位置,也有一个速度,那么我们可以预测一个粒子下一刻的位置

但我们不用这个位置,我们用这两个位置的中点作为中间点,在中间点再用一次欧拉方法,就可以一定程度的避免欧拉方法的问题

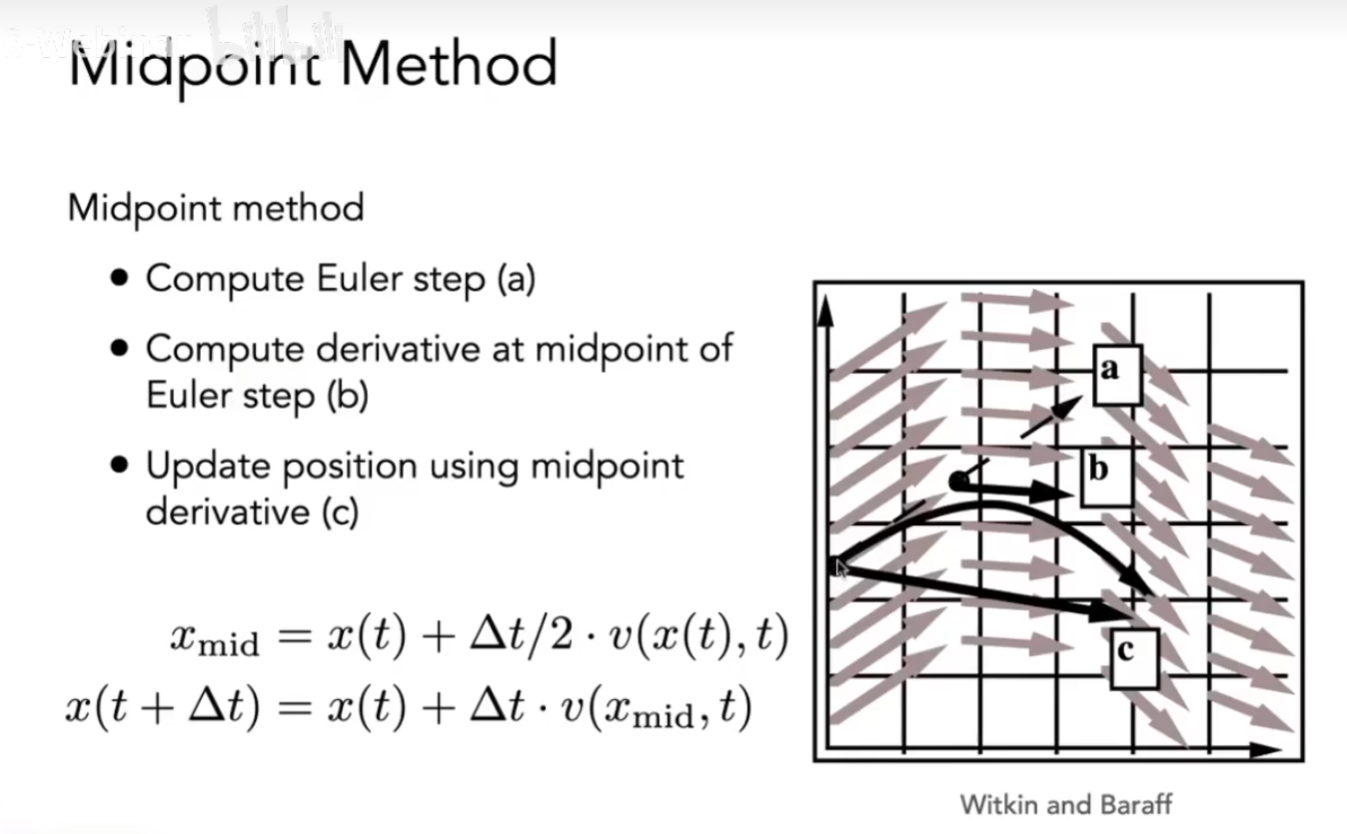
Adaptive Step Size

每次计算位置时,用欧拉方法计算一次位置,再用t/2做两次欧拉方法计算一次位置

如果我们发现两次得到的位置差的不多,就使用后者得到的位置,如果两次得到的位置差的很多,就

继续拆分t,做更多的欧拉方法得到位置

Implicit Euler Method

欧拉方法中,我们用这一帧的速度和加速度计算下一帧的位置

在隐式欧拉方法中,我们用下一帧的速度和加速度计算下一帧的位置

问题在于我们如何得知下一帧的量

Runge-Kutta Families

Runge-Kutta是一类方法,适合解决ODE(微分方程)问题

Rigid Body Simulation

Fluid Simulation

一种简单方法

我们可以将水看成是一堆小球,只要我们能计算小球的位置,我们就可以计算水的位置

在这个方法中,要假设流体是不可压缩的,在任何位置,流体的密度是相同的

Eulerian和Lagrangian

对于一大堆物体的模拟,拉格朗日方法是模拟每一个物体,欧拉方法将空间切成网格

Material Paint Method

MPM方法就是欧拉方法和拉格朗日方法都用

GAMES101常看常新

---

2024/4/8，写过shader之后来复习，GAMES101真的常看常新